|
Question 470288: How do I check my answer for this problem? How do I check for for extraneous solutions. What is extraneous solution? How does it happen?
sqrt(x+3)=x+1
Found 2 solutions by Theo, ewatrrr:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! sqrt(x+3) = x+1
square both sides to get:
x+3 = (x+1)^2
subtract (x+3) from both sides of the equation to get:
(x+1)^2 - (x+3) = 0
expand the equation to get:
x^2 + 2x + 1 - (x+3) = 0
simplify to get:
x^2 + 2x + 1 - x = 3 = 0
combine like terms to get:
x^2 + x - 2 = 0
factor to get:
(x + 2) * (x - 1) = 0
solve for x to get:
x = -2
x = 1
you have 2 possible values of x that will satisfy the equation of x^2 + x - 2 = 0
if you go back to your original equation, you will get:
sqrt(x+3) = x+1
when x = -2, this equation becomes sqrt(1) = -1
when x = 1, this equation becomes sqrt(4) = 2
sqrt(4) = 2 is a valid answer.
sqrt(1) = -1 is not because the square root of 1 is equal to 1, not -1.
the equation of sqrt(x+3) = x+1 only looks for the primary root which is the positive root.
while the negative root is a valid answer if the equation was posed another way, it is not valid the way the question was posed.
when you see an original equation like sqrt(x) = y, then y has to be positive.
when you see something like x^2 = y^2, then sqrt(x) = +/- y is valid, meaning that y can be positive or negative.
if your question was original posed as:
x+3 = (x+1)^2, then you would still have gotten x = 1, x = -2, only this time x = -2 would have been valid.
now when you plug those values into the original equation, you get:
x+3 = (x+1)^2 becomes:
4 = 4 when x = 1
1 = 1 when x = -2
there is no conflict where you got sqrt(x+3) = x+1 becomes 1 = -1 because you could only take the positive square root (the principal square root).
here's another reference on principal square root that addresses that problem.
http://www.mathpath.org/concepts/principal.square.root.htm
bottom line is that there is a convention in mathematics as follows:
if the equation says something like x^2 = something, then plus and minus roots are allowed.
if the equation says something like sqrt(x) = something, then only the positive roots are allowed, even though the negative roots are just as valid.
the reference mentions an inverse function.
an example is y = x^2
the graph of that equation would be:
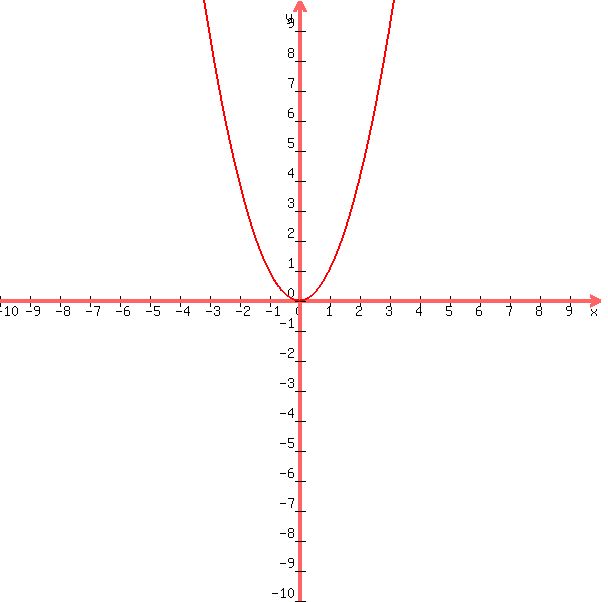
to derive the inverse function, we solve for x and then replace x with y and replace y with x.
our equation of y = x^2 becomes:
x^2 = y
x = +/- sqrt(y)
we replace x with y and y with x to get:
y = +/- sqrt(x)
a graph of this equation gets us:

while this is accurate, it is not a function because you can have multiple values of y for the same value of x (2 values of y for each value of x to be exact).
so we only take the positive square root of y to get:
y = sqrt(x).
our domain had to be positive to start with because sqrt(-x) is invalid, i.e. you can't take the square root of a negative number.
so, only values of x >= 0 are valid for the inverse equation.
suppose, then, if x = 4.
y = sqrt(x) = sqrt(4) = 2
y does not equal -2, even though (-2)^2 = 4.
we only took the positive square root of y, or the principal root of y, and we did not allow the negative square root of y.
y = -2 is valid, but, by convention, we don't allow it, because then our inverse function is not really a function, but a relation.
this makes the root of y = -2 invalid.
the inverse equation now becomes y = sqrt(x), rather than y = +/- sqrt(x).
a graph of that equation is shown below:
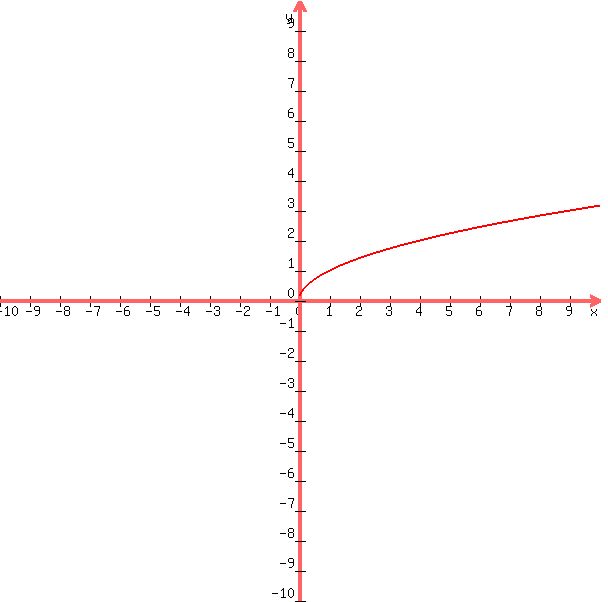
note that the inverse equation is now a function because there is only 1 value of y for each value of x.
FOR PRACTICAL PURPOSES, YOU JUST HAVE TO REMEMBER:
y^2 = x leads to a solution of y = +/- sqrt(x).
y = sqrt(x) leads to a solution of y = + sqrt(x) only.
your equation started off as:
sqrt(x+3) = x+1
this means that you are to get the principal (positive) root only.
that is why the root of x = -2 was invalid, and therefore extraneous.
here's a couple of references that address the extraneous root issue:
http://www.mathwords.com/e/extraneous_solution.htm
http://mathcentral.uregina.ca/qq/database/qq.09.02/paul2.html
http://mathmistakes.info/facts/AlgebraFacts/learn/ctm/extra.html
these cases point up invalid solutions.
sometimes the solutions are valid, but can't be used because of domain restrictions.
the case of the length of a side would be such a restriction.
if the value of x has to be positive, then clearly a negative value of x would be invalid.
also the domain might now allow a division by 0, so if the value of x obtained as a solution makes the original equation be divided by 0, then that solution is also invalid.
always check your solutions against the ORIGINAL equation.
the particular equation you posed does not appear to have an extraneous solution unless there are some restrictions you didn't provide.
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi,
Question states***
sqrt(x+3)=x+1
(x+3) = (x+1)^2
x+3 = x^2 + 2x+ 1
x^2 + x - 2 = 0
factoring
(x +2)(x-1) = 0
(x +2)= 0 x = -2
(x-1) = 0 x = 1
CHECKING our Answers***
sqrt(1)≠ -1, x= -2 is an Extraneous solution
sqrt(4) = 2 x = 1 is the Solution
|
|
|
| |