Question 470220: i) Sketch on the same diagram the graphs of y = |2x + 3| and  .
ii) Find the values of x for which x + |2x + 3| = 1
*Please answer as soon as possible and also please explain in details how your sketch the graph. :) =)
Answer by josmiceli(19441)   (Show Source):
You can put this solution on YOUR website! You can think of  as
the same as  , except that
whenever  is negative, you just ignore the
minus sign and make positive.
-------------------------------
Note that  when  , since
-----------
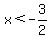When  , then
becomes negative, but you just ignore the minus sign.
Graphically, that amounts to reflecting the line
about the y-axis so that ends up positive
-----------
Here's the graph so far:
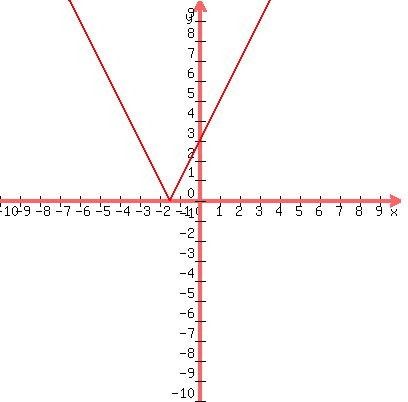
and, adding  ,
Now I want all  for which 
Now subtract from both sides
This is just the solutions, or intersections of the graphs.
---------------------
The reflected part of will have slope = 
and the y-intercept is  so the equation is 
So I want the solutions to:
(1)
(2) 
(3)
(3) and (1):
and
(-2/3, 5/3) is a solution
---------------------
(3) and (2):
and
(-4, 5) is a solution
The answer to (II) is 
and 
|
|
|
