Question 470160: What must be added to x^(3) - 3x^(2) -12x +19 so that the result is exactly divisible by x^(2) + x -6?
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! we have to find polynomials 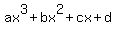 to add to to add to 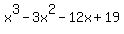 so that the sum is divisible by so that the sum is divisible by  . .
==> -3 and 2 are roots of the divisor  . .
Now  . .
By the factor theorem,
after substituting -3 into the preceding polynomial and simplifying, we must have
27a - 5b + 5c - d = 1;
after substituting 2 into the preceding polynomial and simplifying, we must have
8a +4b + 2c + d = 9;
Adding both equations, we get 7a - b + c = 2, or b = 7a + c - 2.
Substituting this into 8a +4b + 2c + d = 9, we get d = -36a - 6c + 17.
The values for a and c are free to vary.
As an example, let a = c = 1. ==> b = 7*1 + 1 - 2 = 6, and
d = -36*1 - 6*1 + 17 = -25
Then 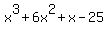 , when added to , when added to 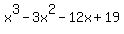 , will be divisible by , will be divisible by 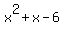 . .
|
|
|