Question 469101: Use the rational zero theorem and quotient polynomials to find all roots of the given equation
12x(^4) + 4x(^3)-17x^+6x=0
(12x to the fourth plus 4x to the third minus 17x squared plus 6x=0)
Answer by lwsshak3(11628)   (Show Source): (Show Source):
You can put this solution on YOUR website! Use the rational zero theorem and quotient polynomials to find all roots of the given equation
12x(^4) + 4x(^3)-17x^+6x=0
(12x to the fourth plus 4x to the third minus 17x squared plus 6x=0)
...
12x^4+4x^3-17x^2+6x=0
x(12x^3+4x^2-17x+6)=0
one of the roots=0
other possible rational roots:
factors of a0=6: ±1, ±2, ±3, ±6
factors of a3=12:±1, ±2, ±3, ±4 ±6, ±12
Possible rational roots: (Divide factors of 6 by factors of 12, exclude duplicates)
±1, ±1/2, ±1/3, ±1/4, ±1/6, ±1/12
±2/3, ±1/6
±3/2, ±3/4
±6
..
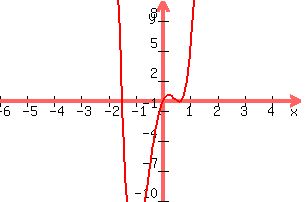
For locating the real number roots, you need to apply the Location Theorem Rule and the Upper and Lower Bound Theorem, but they are too complex to adequately describe with this format. However, with a graphing calculator, you can find that the real roots of the given equation are: -3/2, 0, 1/2, and 2/3. See the graph below.
..
|
|
|