Question 468367: Hi I was hoping someone could Please help me with this problem! Thank you so much!! :)
Movies A survey of 350 customers was taken at Regal Cinemas in Austin, Texas, regarding the type of movies customers liked. The following information was determined.
196 liked dramas.153 liked comedies.
88 liked science fiction.
59 liked dramas and comedies.
37 liked dramas and science fiction.
32 liked comedies and science fiction.
21 liked all three types of movies.
Of the customers surveyed, how many liked
a)none of these types of movies?
b)only dramas?
c)exactly one of these types of movies?
d)exactly two of these types of movies?
e)dramas or comedies?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! The general formula for the union of 3 sets is:
(A union B union C) = A + B + C - (A intersect B) - (A intersect C) - (B intersect C) + (A intersect B intersect C).
We will assign the following:
A = drama
B = comedy
C = science
A intersect B = drama + comedy = AB
A intersect C = drama + science = AC
B intersect C = comedy + science = BC
A intersect B intersect C = dramw + comedy + science (all 3) = ABC
We will now assign numbers to each of these sets:
A = 196
B = 153
C = 88
AB = 59
AC = 37
BC = 32
ABC = 21
We plug these numbers into the formula and we get:
A union B union C = 196 + 153 + 88 - 59 - 37 - 32 + 21
This becomes:
A union B union C = 330
Since there are 350 customers who were surveyed, that leaves 20 who did not like any of the selections.
We need to separate out the categories a little better in order to answer the rest of the questions.
We'll start with ABC.
There are 21 in that category.
We'll then move up to AB, AC, and BC.
Those categories each include ABC so we'll need to remove them from each of those categories.
AB = 59 - 21 = 38 that are in AB only.
AC = 37 - 21 = 16 that are in AC only.
BC = 32 - 21 = 11 that are in BC only.
We'll then move up to A, B, and C.
Those categories each include AB, AC, BC, and ABC.
We'll need to remove them to get A only, B only, C only.
We need to remove AB, AC, and ABC from A to get:
A DISABLED_event_only= 196 - 38 - 16 - 21 = 121.
We need to remove AB, BC, and ABC from B to get:
B DISABLED_event_only= 153 - 38 - 11 - 21 = 83
We need to remove AC, BC, and ABC from C to get:
C DISABLED_event_only= 88 - 16 - 11 - 21 = 40
We have now separated all these groups so there is no double counting in any of the groups.
We have:
A DISABLED_event_only= 121
B DISABLED_event_only= 83
C DISABLED_event_only= 40
A intersect B DISABLED_event_only= 38
A intersect C DISABLED_event_only= 16
B intersect C DISABLED_event_only= 11
A intersect B intersect C = 21
NOT (A union B union C) = 20 (don't like any of the 3 selections).
We add these all up and we get a total of 350 customers.
A Venn Diagram of these sets is shown below:
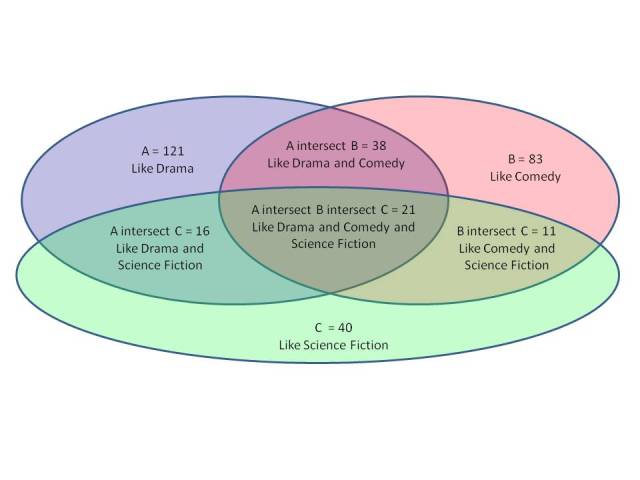
There are a total of 330 customer in this Venn Diagram.
The 20 customer who did not have a preference are not shown.
This checks out with what we were told up front, so we probably did it right.
In removing the double counting, you have to work from the bottom layer up.
The bottom layer was A intersect B intersect C
The next bottom layer was A intersect B, A intersect C, B intersect C.
The top layer was A, B, and C
The higher layers include elements in the lower layers.
A intersect B intersect C was the lowest layer because it didn't include any sets that were part of it.
A intersect B, A intersect C, B intersect C were above ABC because they included ABC as part of their sets.
etc.
Your questions should be able to be answered now.
Those questions are:
a)none of these types of movies?
20
b)only dramas?
121
c)exactly one of these types of movies?
This would be A only plus B only plus C DISABLED_event_only= 121 + 83 + 40 = 244
d)exactly two of these types of movies?
This would be AB only + AC only + BC DISABLED_event_only= 65
e)dramas or comedies?
This would be A only + B only + AB only + AC only + BC only + ABC = 121 + 83 + 38 + 16 + 11 + 21 = 290.
It includes A only because they like drama.
It include B only because they like comedy.
It includes AB only because they like drama and comedy.
It includes AC only because they like drama.
It include BC only because they like comedy
It includes ABC only because they like drama and comedy.
The only category it does not include is C only. Those customers only like Science.
|
|
|