Question 467363: Could you help me with this tough question?
"An open box is to be constructed from 84 square inches of material. What should be the dimensions of the base if the height of the box is to be 2 inches? Surface Area: 
Found 2 solutions by Theo, ankor@dixie-net.com:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! If you are just looking for surface area, then the solution by Ankar is correct.
you have 84 square inches of surface area and you are removing 16 square inches of surface area and you are left with 68 square inches of surface area.
If you are assuming that the bottom of the box is square, than Ankar is correct again.
You start with 84 square inches.
You take the square root of 84 to get 9.16515139 inches on a side.
That means your length is 9.16515139 inches and your Width is 9.16515139 inches.
You remove a 2 inch by 2 inch section from each of the 4 corners.
You then fold up the flaps on each end that are 2 inches in width. These will form the sides of the box that are 2 inches in height.
You are left with a box that has a length of 5.16515139 inches and a width of 5.16515139 inches and a height of 2 inches.
If you let L = length and W = width and H = height, then the formula for Volume (V) and for Surface Area (SA) will be:
V = L * W * H
SA =(L * W) + (2 * H * L) + (2 * H * W)
This comes out to be:
V = 5.16515139 * 5.16515139 * 2 = 53.35757776 cubic inches.
SA = (5.16515139 * 5.16515139) + (2 * 2 * 5.16515139) + (2 * 2 * 5.16515139) = 68 square inches.
If you recall what Ankar said, the Surface Area should be:
84 square inches minus 16 square inches = 68 square inches.
Since we also came up with a Surface Area of 68 square inches the long way, we're good.
Since L = W because the bottom of the box is square, then we can change the formulas around just a little.
We'll let S represent L and S represent W.
S means Side.
Your formula for Volume will change as follows:
V = L * W * H becomes:
V = S * S * H which becomes:
V = S^2 * H.
Your formula for Surface Area will change as follows:
SA = (L * W) + (2 * H * L) + (2 * H * W) becomes:
SA = (S * S) + (2 * H * S) + (2 * H * S) which becomes:
SA = S^2 + (4 * H * S)
Written without the multiplication signs, this becomes:
SA = S^2 + 4HS
If you replace H with h and you replace S with x, then you get:
SA = x^2 + 4xh
That's the formula you showed above, so we're doing the right thing.
The formula you showed said that S = x^2 + 4xh.
Replace SA with S and you have your formula.
Ankar is right to assume the bottom of the box is square.
It can only be square if all the sides are of equal length.
It can only be square, if the formula for Surface Area is as shown.
You were asked to find the value of x.
The value of x is equal to 5.16515139
This was the value of L and W and, subsequently S, that we found above..
This can be rounded to whatever number of decimal places you require.
If no rounding is required, then leave it as is.
Round to:
1 decimal place and x = 5.2
2 decimal places and x = 5.17
3 decimal places and x = 5.165
4 decimal places and x = 5.1652
etc.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! "An open box is to be constructed from 84 square inches of material.
What should be the dimensions of the base if the height of the box is to be 2 inches?
Surface Area: S = x^2 + 4xh
height is given as 2", therefore
SA = x^2 + 4x*2
SA = x^2 + 8x
:
The base is square, therefore the material is square
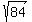 = 9.165" square = 9.165" square
x = 9.165 - 2(2); subtract the 2" used for the 2" height on each side
x = 9.165 - 4
x = 5.165" length and width of the base
Surface area
SA = 5.165^2 + 8(5.165)
SA = 26.677 + 41.32
SA = 68 sq/inches, surface area of the box
:
:
We can check this, 4 each 2" squares removed to accomplish this
Total area of these squares: 4(4) = 16
Box area plus 2" square areas should = the original material area
68 + 16 = 84
:
:
It just dawned me we could have done this in our head. Given the height is 2" we know that 4 ea 2" squares will be removed for a total of 16 square inches.
What remains, is the surface area of the box, 84-16 = 68 sq/inches!
|
|
|