Question 467298: I can figure this problem out, except for the last part of the question: the book answers the year of 2039, how do they come up with that from the equation?b) use the function to find out when the number of people 100 years or older will reach 100,000 What am I doing wrong?
Thanks so much
In recent years, the number of people in the united states who are 100 years old and older can be estimated by the function p(t) = 1.32t-2589.5
t= the year
p(t)= the number of people, in thousands, who are 100 or older
a) Find p(2010). Find p(2020)
p(2010) =1.32(2010)-2589.5 = 63.7
p(2020) =1.32(2020)-2589.5= 76.9
b) use the function to find out when the number of people 100 years or older will reach 100,000
100,000= 1.32(t)- 2589.5
2589.5+100,000=1.32t
102589.5=1.32t 102589/1.32=77719.32
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Sorry about this idiot on here today.
:
The number of persons over 100 yrs is given in 1000s, therefore 100,000 is 100
:
Your solutions would mean 63,700 and 76,900
:
b) use the function to find out when the number of people 100 years or older will reach 100,000
this would be:
100 = 1.32(t)- 2589.5
2589.5 + 100 = 1.32t
2689.5 = 1.32t
t = 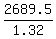
t = 2037.5 ~ 2038, not quite what the book says, but I think this is right
|
|
|