Question 467123: the degree of a polynomial p(x)is no larger than 3. we know that p(0)=3,
P(-x)=p(x), and p(1/x)=p(x)/x2. find p(1)?
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let M =  . .
Then M + 461 =  . .
Subtract the top equation from the bottom equation, to get

<==> 
==> 461 = 2x + 1
==> 2x = 460
==> x = 230.
Hence M = 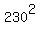 = 52,900. = 52,900.
------------------------------------------------------------------------------
We must have  , ,
p(0) = 3, p(-x) = p(x),  . .
Let 
==> p(0) = d = 3, as given.
Now 
==> a = 0 by direct correspondence of terms,
b = d, and c is some real number.
==> b = d = 3, and a = 0.
==> 
Now p(x) = p(-x) ==> 
==> cx = -cx ==> 2cx = 0.
Since x is not zero for all values of x in the domain of p(x), this means that c = 0.
Therefore  and and  . .
|
|
|