Question 467010: Find the exact value of sin(2q) if csc(q) = -4 and 180° < q < 270°
Found 2 solutions by stanbon, Edwin McCravy:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! Find the exact value of sin(2theta) if csc (theta) = -4 and 180
---
csc = r/y = -4/1
---
So, r = 4 and y = -1
--
Then x = sqrt[4^2 - 1^2] = sqrt(15)
---
Note: x may be positive or negative depending
on whether theta is in the 3rd or 4th Quadrant
---
sin(2theta) = 2sin(theta)*cos(theta)
---
If x is negative, cos(theta) = x/r = -sqrt(15)/4
and sin(2theta) = 2(-1/4)(-sqrt(15)/4) = sqrt(15)/8
======================================================
If x is positive, cos(theta) = x/r = sqrt(15)/4
and sin(2theta) = 2(-1/4)(sqrt(15)/4) = -sqrt(15)/8
============
Cheers,
Stan H.
----
Answer by Edwin McCravy(20056)  (Show Source):
You can put this solution on YOUR website!
Find the exact value of sin(2q) if csc(q) = -4 and 180° < q < 270°
The other tutor said incorrectly that x could be positive or negative.
That's because he ignored that you said 180° < q < 270°. This pinpoints q squarely in the
third quadrant, where x is clearly negative and not positive.
We use the formula sin(2q) = 2sin(q)cos(q)
But we will need sin(q) and cos(q)
Let's draw the picture of angle q in standard position in the
3rd quadrant, since 180° < q < 270°.
Since the cosecant is the hypotenuse over the opposite and we
have 4/1, we can draw the terminal side r to be r=4 units long.
Now we draw a perpendicular from the end of the terminal side up
to the x-axis, like this, and it will be y=-1 because the cosecant
is r/y, and since cosecant is -4 and r=-4, y=-1, and
__
Now we see that x = -Ö
15, y = -1, and r = 4
So sin(q) =  =  and cos(q) =  =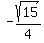 
and we can substitute in
sin(2q) = 2sin(q)cos(q)
and get
Edwin
|
|
|
