Question 466550: heather is twice as old as armida while kaye is 35 years youner than heather. if 1/2 the age ofarmida 5 years ago , and 1/3 of the age of heathr 10 years from now is twice the age of kaye, how old is kaye now?
Answer by ankor@dixie-net.com(22740)   (Show Source):
You can put this solution on YOUR website! Heather is twice as old as Armida while Kaye is 35 years younger than Heather.
If 1/2 the age of Armida 5 years ago, and 1/3 of the age of Heather 10 years from now, is twice the age of Kaye, how old is Kaye.
:
Let h = Heather's present age
Let a = Armida's
Let k = Kaye's
:
Write an equation for each statement:
:
"Heather is twice as old as Armida"
h = 2a
or
a = .5h
:
"while Kaye is 35 years younger than Heather."
k = h - 35
or
h = (k+35)
:
we need to get a in terms of k also
a = .5(k+35)
a = (.5k+17.5)
:
"If 1/2 the age of Armida 5 years ago, and 1/3 of the age of Heather 10 years from now, is twice the age of Kaye,"
 (a-5) +  (h+10) = 2k
:
multiply by 6 to clear the denominators, results:
3(a-5) + 2(h+10) = 6(2k)
3a - 15 + 2h + 20 = 12k
3a + 2h + 5 = 12k
replace h with 2a
3a + 2(2a) + 5 = 12k
3a + 4a + 5 = 12k
7a + 5 = 12k
Replace a with (.5k+17.5))
7(.5k+17.5) + 5 = 12k
3.5k + 122.5 + 5 = 12k
3.5k + 127.5 = 12k
127.5 = 12k - 3.5k
127.5 = 8.5k
k =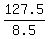 
k = 15 yrs is Kaye's age
:
:
A lot of chances to make a mistake here, check this:
h = 15 + 35 = 50
a = .5(50) = 25
Use these values in the statement:
"If 1/2 the age of Armida 5 years ago, and 1/3 of the age of Heather 10 years from now, is twice the age of Kaye,"
(25-5) + (50+10) = 2(15)
(20) + (60) = 30
10 + 20 = 30; confirms are solution
|
|
|
