|
Question 466530: What is the domain of 
Found 2 solutions by Theo, richard1234:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! The equation is 
the expression within the square root sign can't be negative.
since we are dealing with x^2 within the square root sign, then any real number can be substituted for x and the result will be positive.
therefore, the domain of this equation is the set of all real numbers.
to give you some examples:
x = -5, then y = sqrt(27) which is a positive number within the sqrt sign.
x = 0, then y = sqrt(2) which is a positive number within the sqrt sign.
x = 5, then y = sqrt(27) which is a positive number within the sqrt sign.
the domain is the set of all real numbers.
SINCE YOU WERE ONLY ASKED TO FIND THE DOMAIN, YOU CAN STOP HERE.
IF YOU ARE INTERESTED, YOU MAY CONTINUE TO THE DISCUSSION ON THE RANGE SHOWN BELOW:
the range (value of y, given the value of x) is the set of all real numberS >= sqrt(2).
that's because the number within the square root sign will never be less than 2.
a graph of this equation is shown below:

note that the result of this equation is the principal, or positive square root of the expression only.
that's because the radical sign is part of the equation.
even though the negative square root is also valid, it is not part of the range of this equation because of the existence of the radical sign, which forces the answer to be the positive square root only.
a reference that explains this sometimes confusing situation is shown below.
http://www.helpalgebra.com/onlinebook/roots.htm
because the radical sign implies the positive, or principal, square root only, then, when you are asked to solve the equation y =  , the answer is plus 2, and when you are asked to solve the equation y^2 = 4, then the answer is plus or minus 2. , the answer is plus 2, and when you are asked to solve the equation y^2 = 4, then the answer is plus or minus 2.
in the first case, the radical sign forced the answer to be the principal, or positive square root only. in the second case, the fact that there was no radical sign in the equation allowed the answer to be both the principal and the negative square root.
if your equation were:
y^2 = x^2 + 2, then the answer would have been y = plus or minus 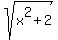 and the graph would have looked like this: and the graph would have looked like this:

in that case, the domain (the value of x) would have still been the set of all real numbers, but the range would have been x >= sqrt(2) or x <= -sqrt(2).
note the special case of y = 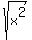 in the reference. in the reference.
the reference states that y =  = 5 = 5
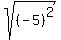 = |-5| = 5 = |-5| = 5
without this rule, then the square root of (-5)^2 could have been interpreted as being equal to (-5) because the square root of x^2 = x. the rule forces the answer to be the principal root only, even through the original root was negative.
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! Function is defined everywhere, because x^2 is nonnegative for all real x, so x^2 + 2 is always positive (x^2 + 2 >= 2), and the square root expression is defined.
|
|
|
| |