Question 465430: Suppose A and B are events with P(A) = 1/4, P(B) = 2/5, and P(A or B) = 1/2.
a) Are the events A and B mutually exclusive? Explain your reasoning.
b) What is P(A and B)?
c) Are the events A and B independent? Explain your reasoning.
Found 2 solutions by robertb, stanbon:
Answer by robertb(5830)   (Show Source):
You can put this solution on YOUR website! a) Two events A and B are mutually exclusive if P(A) + P(B) = P(A U B).
P(A) + P(B) = 1/4 + 2/5 = 13/20, but P(A U B) = P(A or B) = 1/2, so 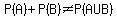 , so A and B are not mutually exclusive.
b) P(A and B) = P(A) + P(B) - P(A or B) = 3/20 = 0.15
c) Two events A and B are independent if P(A)*P(B) = P(A and B).
 , so A and B are not independent.
Answer by stanbon(75887)  (Show Source):
You can put this solution on YOUR website! Suppose A and B are events with P(A) = 1/4, P(B) = 2/5, and P(A or B) = 1/2.
a) Are the events A and B mutually exclusive? Explain your reasoning.
no as you can see in the answer to "b" (below).
----------------------------------------------
b) What is P(A and B)
= P(A) + P(B) - P(A or B)
= (1/4) + (2/5) - (1/2)
= (13/20)- (10/20) = 3/20
-------------------------------------------------
c) Are the events A and B independent?
Check: P(A)*P(B) = P(A|B) ???
(1/4)(2/5) = P(A and B)/P(B) ???
2/20 = (3/20)/(2/5) ???
1/10 = 6/100 ???
Answer: 1/10 does not equal 3/50
So A and B are not independent.
===================================
Cheers,
Stan H.
|
|
|
