Question 461960: Astronomers can use the brihtness of two light sources,such as stars, to compare the distances from the light sources.The intensity , or brightness, of light I is inversely proportionnal to the square of the distance from the light source d.
a) rite an qution that represents this sititution.
b) if d is the independent variable and I is the dependent variable,graph the rqution from exercise a when k=16
c) if two people are viewing the same light source,and one person is three time the distance from the light source as the other person,compare the light intensities t
page 470#42
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Astronomers can use the brihtness of two light sources,such as stars, to compare the distances from the light sources.The intensity , or brightness, of light I is inversely proportionnal to the square of the distance from the light source d.
a) write an equation that represents this situation.
Ans: I = k/d^2
-----------------------
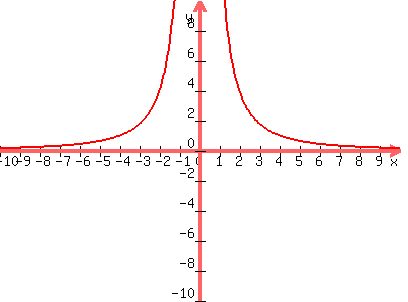
b) if d is the independent variable and I is the dependent variable,graph the equation from exercise a when k=16
I = 16/d^2
------------------
-----------------------------------------------
c) if two people are viewing the same light source,and one person is three times the distance from the light source as the other person,compare the light intensities t
--
intensity for person closer to sight source = k/d^2
intesity for person further away = k/(3d)^2
---
Compare the two by dividing: [k/d^2]/[k/(3d)^2] = (k/d^2) = 9
----
The intesity for the person closer to the light source
is 9 times as great as for the person further away from
the light source.
============
Cheers.
|
|
|