Question 461625: hi am stuck on a question on theory of numbers
a, b, c, c, are four unequal positive numbers. by using the theorem (if a=b, then a+c=b+c and ac=bc) and considering the first pair of numbers 1/2(a+b) and 1/2(c+d) and then separately, the pairs a,b and c,d prove that
1/4(a+b+c+d)>(abcd)^1/4
Deduce by considering the four unequal numbers a,b,c and 1/3(a+b+c)that
1/3(a+b+c)>(abc)^1/3
what happens to the last inequality (i) if a=b=c
(ii)if a=b≠c?
suggest a generalization of the results proved above?
Phew this is one of the toughest questions i have ever come across?
Answer by Edwin McCravy(20060)   (Show Source):
You can put this solution on YOUR website!
Since the inequality we are to prove for the letters
representing unequal positive numbers:
and one of the other parts is
Then we might suppose that the first thing we need to
prove is that for any different positive numbers a and b
The technique I will use is to assume that it is false,
and then reach a contradiction.
So for contradiction we will assume that for  ,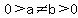
Multiply both sides by 2
Square both sides:
Subtract 4ab from both sides:
Factor the left side:
This is false since the left side is positive,
since a and b are different.
So we have reached a contradiction and therefore
we have proved that
Note that the two sides are equal if a=b.
We have also proved by letting a=c and b=d.
that for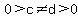 
Down below we will need this for positive x,y:
with equality holding if and only if x=y.
We do this to avoid getting letters confused.
--------------------------------
Next we will prove that for a,b,c,d > 0, all different,
We start with
Multiply both sides by 2, and we have:
Add the two inequalities:
Factor out 2 on the right
Make the left side into the left side of what
we have to prove by multiplying thru hy 1/4
Now we will show that the right side is greater than or equal
to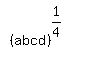 
We recall from above that for positive x, y,
with equality holding if and only if x=y
We let x = 
and y = 
[Notice that we had to include the possibility of equality
since even though a,b,c,d are all distinct, that does not
guarantee that
and
are distinct, e.g. if a=1,b=6,c=2,d=3, they are not distinct.]
So we have proved:
which is what we had to proved.
---------------------------------------
For different positive a,b,c, we need to prove
Sorry, I haven't figured out how to do this one yet.
------------------------------------
The generalization. If all ai are
positive numbers, then
and equality holds only when all the ai are equal.
Edwin
|
|
|
