|
Question 460794: can someone please help me find the inequality for 8+x>3+4 and show how you got the answer.
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! You can work these problems using similar methods that you learned for solving equations ... EXCEPT ... if you have to multiply or divide both sides by a negative number, you need to reverse the direction of the inequality sign.
.
With that in mind, let's work your problem. Given:
.
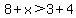
.
(Remember just think of the > as an = sign an use the rules for solving equations)
.
Add the two numbers on the right side to get:
.
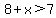
.
Get rid of the 8 on the left side by subtracting 8 from both sides:
.
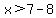
.
Combine the two numbers on the right side by subtracting 8 from 7:
.
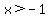
.
That's the answer. x is greater than negative 1. So on the number line, x is any number to the right of -1.
.
Do a few quick checks to see if this works. Suppose x = 0. Go to the original problem and substitute 0 for x. Does the inequality hold true?
.
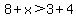
.
becomes:
.
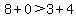
.
or
.

.

.
Looks good because 8 is greater than 7. What about letting x = -2? The original problem becomes:
.
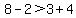
.
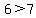
.
Whoops. 6 is not greater than 7, so x cannot equal -2. That still agrees with the solution which was that x had to be greater than -1. So our answer looks good from these two simple checks. You can do more checks just to build your confidence in the answer by using more values for x on either side of -1. If the value of x is to the right of -1 on the number line, it should make the original inequality true. If x is to the left of -1 on the number line, then the original inequality should not work.
.
In this problem you did not have to apply the rule about reversing the direction of the inequality sign because the equation led to a solution for positive (or +) x.
.
However, just supposed that in solving a problem you came up with a negative sign on x. How would you do that? For example, suppose your original problem had been:
.

.
Notice the minus sign on the x. This makes it a new problem and not the same as the original problem you were given. (I made up this problem to show you what to do with MULTIPLYING or DIVIDING both sides by a negative number.) To solve this new problem, begin by adding the two numbers on the right:
.
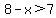
.
Subtract 8 from both sides:
.
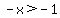
.
What would you do now to solve for +x? Simple. Multiply both sides by minus 1 to change the inequality to:
.
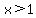
.
But be careful!!! You multiplied both sides by a negative number. Therefore, you need to REVERSE the direction of the inequality sign. When you do that, the real answer becomes:
.
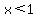
.
And this means that on the number line x can be any value to the left of +1.
.
Try substituting 0 for x and see if the original inequality of
.
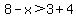
.
works out to be true with zero as the value of x. It should be true because 0 lies to the left of +1.
.
Then try the same process only using +2 as the value of x. The inequality should no longer be true because +2 lies to the right of +1.
.
Hope this helps you to understand the way to solve inequalities a little more.
|
|
|
| |