Question 456884: The sides of a length of a triangle are x, x+4, and 20, where 20 is the longest side. For which range of values is x an acute triangle
Found 2 solutions by spacesurfer, robertb:
Answer by spacesurfer(12)   (Show Source):
You can put this solution on YOUR website! First, a right triangle is the breaking point for acute vs obtuse triangle. We find for what x we have a right triangle. There are two scenarios:
Case 1) x and (x+4) are the two feet and 20 is the hypotenuse or
Case 2) x and 20 are the two feet and (x+4) is the hypotenuse
Note that 20 and (x+4) cannot be the 2 feet since x < x+4.
Case 1)  --> The solution is x = 12 after discarding -16 as a solution.
Case 2)  --> x = 48.
Hence, 12 < x < 48 since, when x = 12, we have a right triangle with sides 12, 16, 20; and when x = 48, we have another right triangle with side 20, 48, 52.
Answer by robertb(5830)  (Show Source):
You can put this solution on YOUR website! For the triangle to be acute, 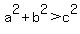 , where c is the longest side of the triangle. Note that it is given that the longest side has length 20.
Hence, we must have  , or , after simplifying,  , or (x+16)(x - 12) >0. Since x must have positive values only, x > 12.
From the triangle inequality, we get the relation x +(x+4) > 20, or x > 8. Also, since 20 is the longest side, we must have x + 4 < 20, or x < 16. Hence from the initial conditions, we must have 8 < x < 16.
Intersect the preceding interval with the interval x > 12.
Therefore, for the triangle to be acute, we must have 12 < x < 16.
|
|
|
