|
Question 456862: You are a star basketball player and receive the following two offers. Which one should you choose and why? There are 82 regular season games in the NBA.)(Hint: Think about the function that each situation represents.)
Option 1: A one billion dollar signing bonus and 1 million dollars per game.
Option 2: A one penny signing bonus with salary to double each game. In other words the salary for the first game is 2 pennies, the salary for the second games is 4 pennies, and so on.
Answer by htmentor(1343)   (Show Source):
You can put this solution on YOUR website! You are a star basketball player and receive the following two offers. Which one should you choose and why? There are 82 regular season games in the NBA.)(Hint: Think about the function that each situation represents.)
Option 1: A one billion dollar signing bonus and 1 million dollars per game.
Option 2: A one penny signing bonus with salary to double each game. In other words the salary for the first game is 2 pennies, the salary for the second games is 4 pennies, and so on.
===================================================================
Option 1: The salaries for each consecutive game represent an arithmetic sequence with common difference = 1000000.
For example, the salary for the first 3 games will be: 1001000000, 1002000000, 1003000000.
The n-th term of an arithmetic sequence can be written:
 , where d is the common difference
For simplicity, we will express our formula in millions of dollars.
So the salary for the n-th game will be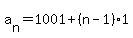 
We can write the cumulative salary earned after game n as:
The sum of this series is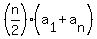 
So the cumulative salary earned after the 82nd game will be:
 [in millions of dollars]
Option 2: In this case, we can describe the game salaries as a geometric
sequence with common ratio 2, since the salary doubles with each successive
game.
In general the sum of an arithmetic sequence can be written:
The sum of this series is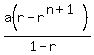 
In this case, a = 1, and r = 2
Therefore the cumulative salary [in pennies] after game n can be written as
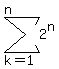
And the sum of this series is given by 
In dollars, the option 2 salary is 
The option 1 salary, in dollars, is 85403*1E6 = 8.54E10
So, without question, the player should choose option 2 [I'd like to be his agent, and get 10% of that!]
|
|
|
| |
