SOLUTION: Given three consecutive integers, what is the difference between the average of their squares and the square of their average?

Algebra ->  Customizable Word Problem Solvers  -> Numbers -> SOLUTION: Given three consecutive integers, what is the difference between the average of their squares and the square of their average?      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 456820: Given three consecutive integers, what is the difference between the average of their squares and the square of their average?
Answer by spacesurfer(12) About Me  (Show Source):
You can put this solution on YOUR website!
Did you try to do this your self? Just do the math:
If a = first integer, then a+1, and a+2 are the other consecutive integers. The average of the squares is:
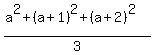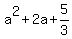
%28a%5E2+%2B+%28a%2B1%29%5E2+%2B+%28a%2B2%29%5E2%29%2F3 = a%5E2+%2B+2a+%2B+5%2F3
The square of the average is:
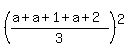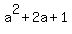
%28%28a%2Ba%2B1%2Ba%2B2%29%2F3%29%5E2 = a%5E2%2B2a%2B1
Hence, the difference is 5/3 - 1 = 2/3.
If the integers didn't increase by 1 and instead increased by b, so like instead of 3,4,5, it was 3, 3+b, 3+2b, for any b (if b = 2, then 3, 5, 7), then the difference is 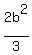2b%5E2%2F3.
if b = 1, then this reduces to 2/3, which we got earlier.