Question 456820: Given three consecutive integers, what is the difference between the average of their squares and the square of their average?
Answer by spacesurfer(12)   (Show Source): (Show Source):
You can put this solution on YOUR website! Did you try to do this your self? Just do the math:
If a = first integer, then a+1, and a+2 are the other consecutive integers. The average of the squares is:
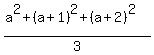 = = 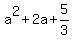
The square of the average is:
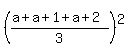 = = 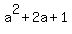
Hence, the difference is 5/3 - 1 = 2/3.
If the integers didn't increase by 1 and instead increased by b, so like instead of 3,4,5, it was 3, 3+b, 3+2b, for any b (if b = 2, then 3, 5, 7), then the difference is 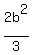 . .
if b = 1, then this reduces to 2/3, which we got earlier.
|
|
|