Question 45662: Hi again,
I need some assistance with this mixture problem:
It takes a pipe 10 minutes less than another one to fill a tank of water. Both pipes together can fill the tank in 12 minutes. How long will it take each one to fill the tank separately?
I am having trouble on how to start setting the equation up.
Thanks again,
Lou
Found 4 solutions by Fermat, stanbon, MathTherapy, ikleyn:
Answer by Fermat(136)   (Show Source):
You can put this solution on YOUR website! Let the two pipes have fill rates of R1 and R2 m^3/min
Let the volume of the tank be V m^3
The time for pipe1 to fill the tank is,
T1 = V/R1 min
similiarly,
T2 = V/R2
The difference in times is 10 min, so we can write,
T1 - T2 = 10
(at the moment it doesn't matter whether you say T1-T2 or T2-T1, since we haven't said which of R1 and R2 is the greater. It will all work out in the end)
substituting for T1 and T2,
V/R1 - V/R2 = 10
V(1/R1 - 1/R2) = 10
====================
If pipe1 fills the tank at R1 m^3/min and pipe2 fills the tank at R2 m^3/min, then together they both fill the tank at a rate of (R1+R2) m^3/min.
T3 = V/(R1+R2)
12 = V/(R1 + R2)
================
You now have two equations in R1 and R2 from which you can solve for R1 and R2 separately, in terms of V.
You should end up with T1 = 30 mins, T2 = 20 mins.
Answer by stanbon(75887)  (Show Source):
You can put this solution on YOUR website! It takes a pipe 10 minutes less than another one to fill a tank of water. Both pipes together can fill the tank in 12 minutes. How long will it take each one to fill the tank separately?
Faster Pipe DATA:
Time to do the job = x minutes; Rate= (1/x) job/min
Slower Pipe Data:
Time to do the job = x-10 minutes: Rate = 1/(x-10) job/min
Filling Together Data:
Time to do the job = 12 minutes: Rate = 1/12 job/min
EQUATION:
rate + rate = rate together
1/x + 1/(x-10) = 1/12
[x-10+x]/[x(x-10} = 1/12
12(2x-10) = x^2-10x
x^2-34x+120=0
(x-30)(x-4)=0
x= 30 minutes or x= 4 minutes
Only the x=30 minute answer applies because the slower pipe time is then 20 min.
Slower pipe time is 30 minutes.
Faster pipe time is 20 minutes.
Cheers,
Stan H.
Answer by MathTherapy(10585)  (Show Source):
You can put this solution on YOUR website!
Hi again,
I need some assistance with this mixture problem:
It takes a pipe 10 minutes less than another one to fill a tank of water. Both pipes together
can fill the tank in 12 minutes. How long will it take each one to fill the tank separately?
I am having trouble on how to start setting the equation up.
Thanks again,
Lou
Let time it takes FASTER pipe, be F
Then time it takes the SLOWER pipe = F + 10
Fraction of tank filled by FASTER pipe in 1 munute: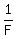 
Fraction of tank filled by SLOWER pipe in 1 munute: 
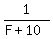With the time taken by both pipes to fill the tank being 12 minutes, we get the following equation: 
12(F + 10) + 12F = F(F + 10) ------ Multiplying by LCD, 12F(F + 10)
(F - 20)(F + 6) = 0
F - 20 = 0 OR F + 6 = 0____F = - 6 (ignore)
Time faster pipe takes to fill tank, by itself, or F = 20 minutes
Time slower pipe takes to fill tank, by itself, or F + 10 = 20 + 10 = 30 minutes
The answer can also be seen HERE ====> Question 742195: One pipe can fill a tank in 20 minutes, while
another takes 30 minutes to fill the same tank. How long would it take the two pipes together to fill the tank?
Answer by ikleyn(53419)  (Show Source):
You can put this solution on YOUR website! .
Hello, in your post you call this problem as a "mixture problem".
Actually, it is not a "mixture" problem and never was.
The problems of this kind have their traditional name, which is "joint work" problems.
Do not create your own names for subjects in the area, where they are well established
just for hundred years and with which you are unfamiliar with.
Making disorder in a well ordered space is not a good style and is disrespect to traditions.
Besides of it, it shows that you don't know a standard terminology,
which is not in your interests to demonstrate around.
|
|
|
