SOLUTION: How do I find the center, vertices, co-vertices, and foci of this ellipse x squared+4y squared-2x+16y+13=0? I tried subtracting 13 to both sides then factoring everything else but

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: How do I find the center, vertices, co-vertices, and foci of this ellipse x squared+4y squared-2x+16y+13=0? I tried subtracting 13 to both sides then factoring everything else but       Log On


   

Question 455942: How do I find the center, vertices, co-vertices, and foci of this ellipse x squared+4y squared-2x+16y+13=0? I tried subtracting 13 to both sides then factoring everything else but it doesn't look right. Can someone help me?
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

Rational Exponents



x%5E2%2B4y%5E2-2x%2B16y%2B13=0...group
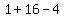
%28x%5E2-2x%29%2B%284y%5E2%2B16y%29%2B13=0.....write 13 as 1%2B16-4
%28x%5E2-2x%2B1%29%2B%284y%5E2%2B16y%2B16%29+-4=0
%28x-1%29%5E2%2B4+%28y%2B2%29%5E2-4+=+0
%28x-1%29%5E2%2B4+%28y%2B2%29%5E2=4+...both sides divide by 4
%281%2F4%29+%28x-1%29%5E2%2B%28y%2B2%29%5E2+=+1.........or


%28x-1%29%5E2%2F4%2B%28y%2B2%29%5E2%2F1+=+1....compare to:
%28x-h%29%5E2%2Fa%5E2%2B%28y-k%29%5E2%2Fb%5E2+=+1...if the major axis runs horizontally
you see that:
h=1
k=-2
a=2
b=1

The center of the ellipse is (h,k) = (1,-2).
The major vertices are (h-a,k) and (h+a,k) or (-1,-2) and (3,-2)

c+=+sqrt%28a%5E2+-+b%5E2%29+=sqrt%284+-+1%29+=+sqrt%283%29+=+1.73
The foci are (h-c,k) and (h+c,k) or
(1-1.73,-2) and (1+1.73,-2) which is (-0.73,-2) and (2.73,-2).