Question 452746: For a triangle with a perimeter of 12 and an area of 7 what are the lengths of the triangles legs?
Is there an equation that relates area and perimeter to give you leg lengths? Or something similar?
Some things I’ve tried:
1: Finding “a” “b” and “c” directly by converting a set of equations into a matrix in row echelon form. The issue is I can’t find a set of linear equations that relate a, b, and c to the triangle.
2: Listing possible solutuions for b and h from the area formula that are also factors of 14. 14 because   . This is impossible because there are an infinite number of possibilities. So I went for positive integers [(b:1,2,7,14)(h:1,2,7,14)]. I didn't continue with this train of thought because something else occured to me. . This is impossible because there are an infinite number of possibilities. So I went for positive integers [(b:1,2,7,14)(h:1,2,7,14)]. I didn't continue with this train of thought because something else occured to me.
3: When a triangle is split into 2 triangles and the line that splits them is perpedicular to one of the lines it touches then both of the triangles are right triangles. The pythagorian therum  works for right triangles. Giving me another equation to work with. I couldn't figure out how to use it though. works for right triangles. Giving me another equation to work with. I couldn't figure out how to use it though.
4:So I square 14 giving me 196. Factoring 196 into primes gave me (2,2,7,7). I made a chart of the ways these numbers could be combined so when they were multiplied i got 14. This gave me 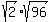 , , 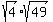 , and , and 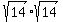 I came to the same problem again as i had with the pythagorean therum; i didn't know how to use the new information. I came to the same problem again as i had with the pythagorean therum; i didn't know how to use the new information.
5: So i went back to the visually drawn triangles and labeled the sides of the original triangle a, b, and c. Then I labeled one of the split triangles sides (the numbers to the right of the letters are subscripts) a1, b1, and c1. The other right triangle was labeled a2, b2, and c2. With the sides labeled i tried to substitute various variables in for each other to see what i could come up with. For example the 2 new triangles both have a side that is equal to (1/2)c from the original triangle so i replace the corresponding variable on the smaller triangle with (1/2)c. I tried many more substitutions like that but none of them yeilded anything I thought I could use.
I am now taking a break from it. And it occurred to me that if there were an equation relating area with perimeter that would be very usefull. Also if there are any other equations that you think might be useful please send those to me as well.
One last thing, please put the things you think might help at the top of the email, and if you know how to solve this kind of problem and include the answer or the "how to" please write something along the lines of "spoiler alert" and skip some lines so it won't be visible. Sorry if i come across as a bit pushy but i really want to figure this one out and then see if i was right.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hint:
The perimeter of a triangle with sides 'a', 'b', and 'c' is  (ie add up the sides to get the perimeter). But you probably already knew that. (ie add up the sides to get the perimeter). But you probably already knew that.
What you probably don't know, or maybe have seen and forgot, is that the area of a triangle with sides 'a', 'b', and 'c' is
 where where  (this is the semiperimeter, which is half the perimeter) (this is the semiperimeter, which is half the perimeter)
Let me know if this is enough to help get you started.
Spoiler Alert:
I don't think there's a solution because solving for a,b, and c gives equations which can be graphed. The graphs can then show where the positive solutions lie. It turns out that not all the solutions are positive, which means that a triangle can't be constructed with these given properties.
|
|
|