SOLUTION: Verify that the points (0,0),(a,0) and (a/2, square root symbol "I don't know how to type it in", with 3a/2 in it, are equilateral triangles. Then show that the midpoints of the th

Algebra ->  Triangles -> SOLUTION: Verify that the points (0,0),(a,0) and (a/2, square root symbol "I don't know how to type it in", with 3a/2 in it, are equilateral triangles. Then show that the midpoints of the th      Log On


   

Question 452054: Verify that the points (0,0),(a,0) and (a/2, square root symbol "I don't know how to type it in", with 3a/2 in it, are equilateral triangles. Then show that the midpoints of the three sides are the vertices of a second equilateral triangle.
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

(0,0),(a,0) and (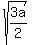a%2F2, sqrt%283a%2F2%29


use Distance formula
(0,0) and (a,0)
D+=+sqrt%28%28a+-+0%29%5E2+%2B+%280+-+0%29%5E2%29
D+=+sqrt%28a%5E2%29
D+=+a

(a,0) and ((a/2),(sqrt((3a)/2))
D+=+sqrt%28%28%28a%2F2%29+-+a%29%5E2+%2B+%28%28sqrt%283%29a%29%2F2%29+-+0%29%5E2%29
D+=+sqrt%28%28%28a%2F2%29+-+%282a%2F2%29%29%5E2+%2B+%28%28sqrt%283%29a%29%2F2%29%5E2%29
D+=+sqrt%28%28-a%2F2%29%5E2+%2B+%28%283a%5E2%29%2F4%29%29
D+=+sqrt%28%28%28a%5E2%29%2F4%29+%2B+%28%283a%5E2%29%2F4%29%29
D+=+sqrt%28%28a%5E2+%2B+3a%5E2%29%2F4%29
D+=+sqrt%28%284a%5E2%29%2F4%29
D+=+sqrt%28a%5E2%29
D+=+a
(0,0) and ((a/2), (sqrt(3)a/2))
D+=+sqrt%28%28%28a%2F2%29+-+0%29%5E2+%2B+%28%28sqrt%283%29a%2F2%29+-+0%29%5E2%29
D+=+sqrt%28%28a%2F2%29%5E2+%2B+%28%28sqrt%283%29a%29%2F2%29%5E2%29
D+=+sqrt%28%28%28a%5E2%29%2F4%29+%2B+%28%283a%5E2%29%2F4%29%29
D+=+sqrt%28%28a%5E2+%2B+3a%5E2%29%2F4%29
D+=+sqrt%284a%5E2%2F4%29
D+=+sqrt%28a%5E2%29
D+=+a
So, since they are 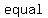all+equal, this is an equilateral triangle.