SOLUTION: Simplify completely {{{ ((Cos(x)+sin(x))^2-(cos(x)-sin(x))^2)/ (2sin(2x)) }}}

Algebra ->  Trigonometry-basics -> SOLUTION: Simplify completely {{{ ((Cos(x)+sin(x))^2-(cos(x)-sin(x))^2)/ (2sin(2x)) }}}       Log On


   

Question 451411: Simplify completely


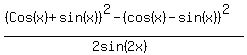
Answer by kingme18(98) About Me  (Show Source):
You can put this solution on YOUR website!
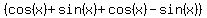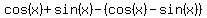The top is a difference of two squares. Remember that +a%5E2-b%5E2=%28a%2Bb%29%28a-b%29+ In your case, a is cos(x)+sin(x), and b is cos(x)-sin(x). Substitute those in and the first parentheses is +%28cos%28x%29%2Bsin%28x%29+%2B+cos%28x%29-sin%28x%29%29+, which simplifies to 2cos(x). For the other, don't forget to distribute the subtraction: +cos%28x%29%2Bsin%28x%29-%28cos%28x%29-sin%28x%29%29+, which simplifies to 2sin(x). 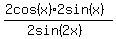Thus, at this point we have: +%282cos%28x%29%2A2sin%28x%29%29%2F%282sin%282x%29%29+.
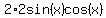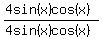The double angle formula for sine says +sin%282x%29+=+2sin%28x%29cos%28x%29+. The denominator is then +2%2A2sin%28x%29cos%28x%29+. If we simplify the numerator and denominator, we have +%284sin%28x%29cos%28x%29%29%2F%284sin%28x%29cos%28x%29%29+, which is, of course, 1 :)