Question 450260: find the vertex, focus, and directrix of the graph of theequation of 12(x-1)=(y+1)^2
Answer by lwsshak3(11628)   (Show Source): (Show Source):
You can put this solution on YOUR website! find the vertex, focus, and directrix of the graph of theequation of 12(x-1)=(y+1)^2
..
This equation is a parabola of the form, (y-k)^2=4p(x-h), with (h,k) being the (x,y) coordinates of the vertex and 4p=coefficient of the x-term.
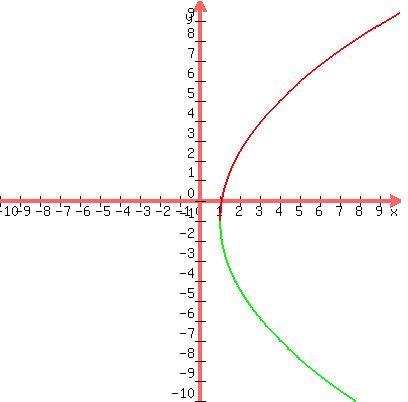
Vertex of given parabola is at (1,-1). It opens rightward with its axis of symmetry on y=-1
4p=12
p=3
The directrix is a line x=-2 (3 units left of the vertex)
The focus is a point on the axis of symmetry 3 units to the right of the vertex at (4,-1)
See the graph below of the equation of the given parabola
..
y=(12(x-1))^.5-1
|
|
|