Question 449383: Hey, Im in much need of help to figure out how to factor/solve qudaratic equations that are not in X^2+bx+c=0 form. for example,how do you factor 4x^2=4x+5?
Found 2 solutions by MathLover1, stanbon:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
factor  ..first write it in ..first write it in  form form

| Solved by pluggable solver: Factoring using the AC method (Factor by Grouping) |
Looking at the expression 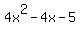 , we can see that the first coefficient is , we can see that the first coefficient is  , the second coefficient is , the second coefficient is  , and the last term is , and the last term is  . .
Now multiply the first coefficient  by the last term by the last term  to get to get  . .
Now the question is: what two whole numbers multiply to  (the previous product) and add to the second coefficient (the previous product) and add to the second coefficient  ? ?
To find these two numbers, we need to list all of the factors of  (the previous product). (the previous product).
Factors of  : :
1,2,4,5,10,20
-1,-2,-4,-5,-10,-20
Note: list the negative of each factor. This will allow us to find all possible combinations.
These factors pair up and multiply to  . .
1*(-20) = -20
2*(-10) = -20
4*(-5) = -20
(-1)*(20) = -20
(-2)*(10) = -20
(-4)*(5) = -20
Now let's add up each pair of factors to see if one pair adds to the middle coefficient  : :
| First Number | Second Number | Sum | | 1 | -20 | 1+(-20)=-19 | | 2 | -10 | 2+(-10)=-8 | | 4 | -5 | 4+(-5)=-1 | | -1 | 20 | -1+20=19 | | -2 | 10 | -2+10=8 | | -4 | 5 | -4+5=1 |
From the table, we can see that there are no pairs of numbers which add to  . So . So 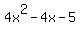 cannot be factored. cannot be factored.
===============================================================
Answer:
So 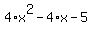 doesn't factor at all (over the rational numbers). doesn't factor at all (over the rational numbers).
So 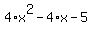 is prime. is prime.
|
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! how do you factor 4x^2=4x+5?
---
Rearrange:
4x^2 - 4x - 5 = 0
----
Using the quadratic formula:
x = [4 +- sqrt(16-4*4*-5)]/(2*4)
---------------------
x = [4 +- sqrt(96)]/8
-----
x = [4 +- 4sqrt(6)]/8
----
r1 = (1/2)+(1/2)sqrt(6) or r2 = (1/2)-(1/2)sqrt(6)
-----
Each of these is a root of the quadratic.
---
The factored form would be (x-r1)(x-r2) = 0
===============================================
So the quadratic formula can ALWAYS be used to factor
a quadratic polynomial.
===============================================
If you are familiar with FOIL, Inverse FOIL can
be used to factor some quadratics.
----
Example:
2x^2+7x-15 = 0
ac = 2*-15 = -30
b = 7
----
Think of 2 numbers whose product is ac and whose sum is b:
ac = 10*-3 = -30
b = 10+ -3 = 7
-----
Rewrite the quadratic replacing the "b-term":
2x^2 + 10x-3x -15 = 0
-----
Factor the 1st two and the last two terms separately:
2x(x+5)-3(x+5) = 0
Factor again:
(x+5)(2x-3) = 0
=============================
Cheers,
Stan H.
=============================
|
|
|