|
Question 449330: how do you put 5x^2-y^2-30x-12y+9=0 into standard graphing form and graph it?
Answer by Math_Teacher_37(4)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Begin by moving all the "x" and "y" terms together, like this:

Now move the "9" to the other side and factor by grouping:
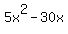 + + 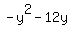 = -9 = -9
For 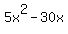 , factor out a "5": , factor out a "5":
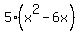
And for 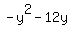 , factor out a "-1": , factor out a "-1":
(to make the number in front of the  term a positive number): term a positive number):
-1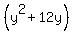
Next, complete the square for 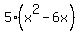 . Remember that you need to take 1/2 of the middle term (1/2*-6 = -3) and square that answer (-3*-3 = 9). Then add this number to the expression to complete the square: . Remember that you need to take 1/2 of the middle term (1/2*-6 = -3) and square that answer (-3*-3 = 9). Then add this number to the expression to complete the square:
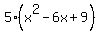
Note that if you distribute the above expression out, you will get the following:
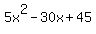 (This means you added 45 to the original expression, something you will need to do to the other side as well.) (This means you added 45 to the original expression, something you will need to do to the other side as well.)
Do the same thing for 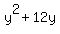 : :
1/2 * 12 = 6
Square 6: 6 * 6 = 36
So, complete the square and get the following:
-1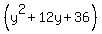
Distribute and get: 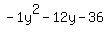
Of course, you will need to add -36 to the other side as well.
In summary, we have added 45 and -36 to both sides of the original equation (and need to add these numbers to the right side as well):
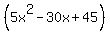 + + 
Simplify:
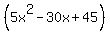 + + 
Factor a "5" out of 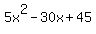 : :
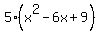 = = 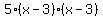
Factor a "-1" out of 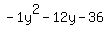 : :
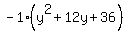 = = 
SO:

Since the right side of the equation equals 0, this conic section is not a hyperbola and cannot be graphed.
|
|
|
| |