Question 449107: Use the point-slope form of the equation y + 4 = 5(x + 6) to identify a point the line passes through and the slope of the line.
answer choices:
a) (−6, −4); 5
b) (−6, −4); −5
c) (6, 4); 5
d) (6, 4); −5
Answer by Leaf W.(135)   (Show Source): (Show Source):
You can put this solution on YOUR website! Point slope form is  . Here, you are looking for ( . Here, you are looking for ( , ,  ) and m, using the equation y + 4 = 5(x + 6) ) and m, using the equation y + 4 = 5(x + 6)
First off, 'm' is fairly easy to find, as it is right outside of (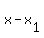 ), or (x + 6). It is 5. ), or (x + 6). It is 5.
Next, find  in in 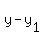 , or y + 4. At first, one might think it is 4, but note that in point slope form there is a minus (y MINUS , or y + 4. At first, one might think it is 4, but note that in point slope form there is a minus (y MINUS  ), but in the equation it is a plus (y PLUS 4). Since two negatives equal a positive, change y + 4 to y - (-4), which more closely follows ), but in the equation it is a plus (y PLUS 4). Since two negatives equal a positive, change y + 4 to y - (-4), which more closely follows 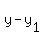 . So, . So,  is -4. is -4.
Finally, Find  in in 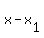 , or x + 6. Note that it is the same kind of deal as with the y (x MINUS , or x + 6. Note that it is the same kind of deal as with the y (x MINUS  versus x PLUS 6), so change x + 6 to x - (-6). So, versus x PLUS 6), so change x + 6 to x - (-6). So,  is -6. is -6.
***THEREFORE, YOUR ANSWER IS a) (-6, -4); 5
|
|
|