Question 448900: write an equation for the conic sections
5. ellipse with center at (0,0) vertex (-4,0) and co-vertex (0,3)
6. circle with center at (-1,2) and radius 4.
7. parabola with vertex at (0,0) and directrix x = -3
8. hyperbola with foci at (-3,0) and (3,0) and vertices at (2,0) and (-2,0)
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi
5. ellipse with center at (0,0) vertex (-4,0) and co-vertex (0,3)

6. circle with center at (-1,2) and radius 4. 
7. parabola with vertex at (0,0) and directrix x = -3
y^2 = (3/4)x 4p = 3 p = 3/4
8. hyperbola with foci at (-3,0) and (3,0) and vertices at (2,0) and (-2,0)
y^2/4 - x^2/5 = 1 c =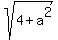 = 3 a = = 3 a = 

Standard Form of an Equation of a Circle is 
where Pt(h,k) is the center and r is the radius
Standard Form of an Equation of an Ellipse is 
where Pt(h,k) is the center and a and b are the respective vertices distances from center.
Standard Form of an Equation of an Hyperbola is  where Pt(h,k) is a center with vertices 'a' units right and left of center. where Pt(h,k) is a center with vertices 'a' units right and left of center.
Standard Form of an Equation of an Hyperbola opening up and down is:
 where Pt(h,k) is a center with vertices 'b' units up and down from center. where Pt(h,k) is a center with vertices 'b' units up and down from center.
Using the vertex form of a parabola,  where(h,k) is the vertex where(h,k) is the vertex
The standard form is  , where the focus is (h,k + p) , where the focus is (h,k + p)
|
|
|