Question 443733: 2sinx-1=0 Can you help me find the general solution to this equation?
Answer by swincher4391(1107)   (Show Source): (Show Source):
You can put this solution on YOUR website! solve for sin(x):
2sinx -1 = 0
2sinx = 1
sinx = 1/2
Draw a 30,60,90 triangle.
Sides (in increasing length), 1,sqrt(3),2
The angles correspond in this way
30 =1
60 = sqrt(3)
hypotenuse = 2
I hope I have accurately described how will draw this triangle.
Locate the angle where its opp/hypo = 1/2.
This is angle 30.
Now remember this mnemonic.
All Students Take Classes.
This means positive values in these quadrants:
Q1 = All
Q2 = Sin
Q3 = Tangent
Q4 = Cosine
We want to know positive 1/2, so in Q1 and Q2 we have positive sin.
Locate the starting angle... it is the angle on the x-axis (horizontal).
In Q1, the starting angle is 0. So 0 + 30 = 30. 30 or  (in radians) is our first angle. (in radians) is our first angle.
In q2, the starting angle is 180. So 180 - 30 = 150 or 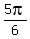 (in radians). (in radians).
So from  we have we have  and and 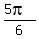 as solutions. But we want to encompass ALL solutions. as solutions. But we want to encompass ALL solutions.
Remember, we can revolve around the circle  radians to end up in the same spot. radians to end up in the same spot.
So the general solution is:
For all integers n,

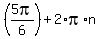
====================
|
|
|