SOLUTION: I am stuck on a project, and am desperate for help. My teacher denied me any help during class, so I'm kind of packed into a corner. 1. I have to write an augmented matrix using t

Get the equations in general form:



The augmented matrix is just an array of all the numbers
in the system without the letters or equal signs:




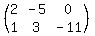That's a 2x3 matrix.

To find two matrices that have a 2x3 matrix as their
product, the first could be a 2x2 and the second a 2x3
matrix. 

Let's make up an arbitrary 2x2 matrix, say



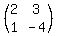Then we'll let the 2x3 matrix be:



So we have



Equating elements of the two 2x3 matrices:, we have 
these 3 systems of equations:

, , , 

We solve those 3 systems and get p=1,s=0, q=-1,t=-1,r=-3,u=2

So one possible answer is




  
But you could make up any (non-singular) 2x2 matrix
and find a 2x3 matrix so that the product would be
equal to the augmented matrix.  There are many possible
answers, in fact infinitely many.

Edwin