Question 442917: A teacher told Melinda that she has a course average of 78 based on her six math tests. When she got home, she found 5 of her tests with scores of 87, 63, 79, 71, and 96. She couldn't find the sixth test. What score did she obtain on that test?
Found 2 solutions by ankor@dixie-net.com, Leaf W.:
Answer by ankor@dixie-net.com(22740)   (Show Source):
You can put this solution on YOUR website! A teacher told Melinda that she has a course average of 78 based on her six math tests.
When she got home, she found 5 of her tests with scores of 87, 63, 79, 71, and 96.
She couldn't find the sixth test. What score did she obtain on that test?
;
Let x = score on the lost test
:
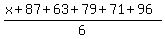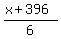 = 78
:
 = 78
Multiply both sides by 6
x + 396 = 6(78)
x + 396 = 468
x = 468 - 396
x = 72 is the score of the lost test
Answer by Leaf W.(135)  (Show Source):
You can put this solution on YOUR website! The average of a set of values is the sum of the values divided by the number of values. In this case (using x as the unknown value/test score), the values are 87, 63, 79, 71, 96, and x. The number of values/test scores is six, and you know that the average is 78. Therefore, you can use the equation  . Next, solve for x:
Multiply both sides of the equation by 6: 
Simplify the right side of the equation by adding the values/test scores together: 
Subtract 396 from both sides to isolate x: 
Therefore, the missing test score must be 72.
|
|
|
