Question 442577: Write an equation of the line containing the given point and perpendicular to give line for:
(7,-7);7x+2y=5
Found 2 solutions by MathLover1, richard1234:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! (7,-7)




| Solved by pluggable solver: Finding the Equation of a Line Parallel or Perpendicular to a Given Line |
Remember, any two perpendicular lines are negative reciprocals of each other. So if you're given the slope of 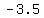 , you can find the perpendicular slope by this formula: , you can find the perpendicular slope by this formula:
 where where 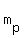 is the perpendicular slope is the perpendicular slope
 So plug in the given slope to find the perpendicular slope So plug in the given slope to find the perpendicular slope
 When you divide fractions, you multiply the first fraction (which is really When you divide fractions, you multiply the first fraction (which is really  ) by the reciprocal of the second ) by the reciprocal of the second
 Multiply the fractions. Multiply the fractions.
So the perpendicular slope is 
So now we know the slope of the unknown line is  (its the negative reciprocal of (its the negative reciprocal of 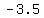 from the line from the line  ).
Also since the unknown line goes through (7,-7), we can find the equation by plugging in this info into the point-slope formula ).
Also since the unknown line goes through (7,-7), we can find the equation by plugging in this info into the point-slope formula
Point-Slope Formula:
 where m is the slope and ( where m is the slope and (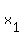 , ,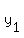 ) is the given point ) is the given point
 Plug in Plug in  , ,  , and , and 
 Distribute Distribute 
 Multiply Multiply
 Subtract Subtract  from both sides to isolate y from both sides to isolate y
 Make into equivalent fractions with equal denominators Make into equivalent fractions with equal denominators
 Combine the fractions Combine the fractions
 Reduce any fractions Reduce any fractions
So the equation of the line that is perpendicular to  and goes through ( and goes through ( , , ) is ) is 
So here are the graphs of the equations  and and 
 graph of the given equation graph of the given equation  (red) and graph of the line (red) and graph of the line  (green) that is perpendicular to the given graph and goes through ( (green) that is perpendicular to the given graph and goes through ( , , ) )
|
so, the line  is perpendicular to is perpendicular to  and containing the given point (7,-7) and containing the given point (7,-7)
Answer by richard1234(7193)   (Show Source): (Show Source):
|
|
|