|
Question 44145This question is from textbook Begining Algebra
: Business and finance. A coffee merchant has coffe beans that sell for $9 per pound and $12 per pound. The two types are to be mixed to create 100 pounds of a mixture that will sell for $11.25 per pound. How much of each type of bean should be used in the mixture.
This question is from textbook Begining Algebra
Found 2 solutions by psbhowmick, adamchapman:
Answer by psbhowmick(878)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let us suppose that the Merchant mixed 'x' lbs of the $9 beans with 'y' lbs of $12 beans.
Hence, he created (x+y) lbs of mixture.
Given, total 100 lbs of the mixture is produced.
So, x + y = 100 _________(1)
Therefore, the cost of (x+y) lbs of the mixture = $(9x+12y).
Hence, the cost of 1 lb of the mixture = $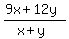 . .
Given, cost of 1 lb the mixture = $11.25.
So, 
or 
or 
or 
or 
or y = 3x ________(2)
Substituting the value of 'y' from (2) in (1) we have
x + 3x = 100
or 4x = 100
or x = 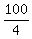
or x = 25
Substituting, x = 25 in (2), y = 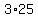 = 75 = 75
Hence, 25 lbs of the $9 beans is to be mixed with 75 lbs of $12 beans to serve the reqd. purpose.
Answer by adamchapman(301)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A = proportion of coffee beans that sell for $9 per pound
B = proportion of coffee beans that sell for $12 per pound
A and B are percentages written in decimal form (e.g. 50%=0.5), and make the whole mix:
A+B=1 ..........................i
The price of the mixture is $11.25 per pound:
A($9)+B($12)=$11.25.............ii
Rearrange equation (i) to give B in terms of A:
B=1-A...........................iii
Substitute equation (iii) into equation (ii) for B:
A($9)+(1-A)($12)=$11.25.........iv
12-3A=11.25
3A=0.75
A=0.25..........................v
Substitute equation (v) into equation (iii) for A to give:
B=0.75
So quarter of the mixture is made of "type A" beans and the remaining three quarters of the mix consists of "type B" beans.
I hope this helps
P.S. I am trying to start up my own homework help website. I would be extremely grateful if you would e-mail me some feedback on the help you received to adam.chapman@student.manchester.ac.uk
|
|
|
| |