9x² + 25y² + 36x - 150y + 36 = 0
9x² + 36x + 25y² - 150y = -36
9(x² + 4x) + 25(y² - 6y) = -36
Multiply the cofficient of x, which is 4, by 1/2, get 2,
square 2, get +4. Add + 4 inside the first parentheses,
which amounts to adding 9*4 or 36 to the left side, so
add + 36 to the right side:
9(x² + 4x + 4) + 25(y² - 6y) = -36 + 36
Multiply the cofficient of y, which is -6, by 1/2, get -3,
square -3, get +9. Add + 9 inside the second parentheses,
which amounts to adding 25*9 or 225 to the left side, so
add + 225 to the right side:
9(x² + 4x + 4) + 25(y² - 6y + 9) = -36 + 36 + 225
Factor the expressions in parentheses
9(x + 2)(x + 2) + 25(y - 3)(y - 3) = 225
Write the factorizations as perfect squares:
9(x + 2)² + 25(y - 3)² = 225
Get a 1 on the right by dividing every term by 225
9(x + 2)² 25(y - 3)² 225
————————— + —————————— = ———
225 225 225
Simplify:
(x + 2)² (y - 3)²
———————— + ———————— = 1
25 9
Compare to
(x - h)² (y - k)²
———————— + ———————— = 1
a² b²
because a² > b² in an ellipse
a² = 25 so a = 5
b² = 9 so b = 3
h = -2, k = 3
center = (h,k) = (-2,3)
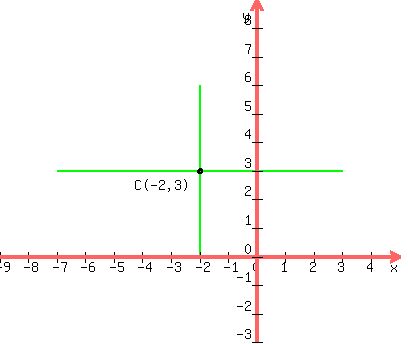
Plot the center:
The major axis is 2a or 2(5) or 10 units long, is horizontal
and has the center as its midpoint. We draw this major axis
in green:
The minor axis is 2b or 2(3) or 6 units long, is vertical
and also has the center as its midpoint. We draw this minor axis
in green also:
We draw in the ellipse:
The vertices are the endpoints of the major axis, (-7,3) and (3,3)
The co-vertices are the endpoints of the minor axis, (-2,0) and (-2,6)
The foci are two points inside the ellips on the major axis, which are
c units from the center on each side of the center. We calculate c from
this equation
c² = a² - b²
c² = 5² - 3²
c² = 25 - 9
c² = 16
c = 4
So the foci are (-6,3) and (2,3)
Edwin
