Question 439478: I am having issues understanding how and when to "reorder the operations". It appears when the reorder of operations is done that all expressions with a letter get moved to the right and all subtraction problems get changed to additions problems. What are the rules of this?
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! first something about the  OF OPERATIONS RULES OF OPERATIONS RULES
When performing more than one operation on an algebraic expression, work out the operations and signs in the following order:
 calculate powers and roots. calculate powers and roots.
 perform all multiplication and division. perform all multiplication and division.
Finally,  with addition and subtraction. with addition and subtraction.
 of operations are a of operations are a  of of 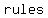 that mathematicians have that mathematicians have 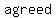 to to 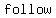 to avoid mass to avoid mass 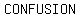 when when  mathematical expressions or equations. mathematical expressions or equations.
easier way to remember the ORDER OF OPERATIONS RULES
For those of you that remember best with acronyms:
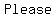 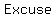 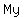 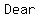 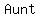 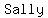 ( (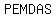 ) )
Please ...=>...Parentheses
Escuse...=>...Exponents
My ...=>...Multiplication
Dear ...=>...Division
Aunt ...=>...Addition
Sally ...=>...Subtraction
now, about the  OF OPERATIONS RULES OF OPERATIONS RULES
the 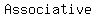 Property, the Property, the 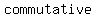 property, and the property, and the 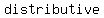 property-three basic properties of numbers- allow you to property-three basic properties of numbers- allow you to 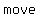 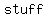 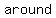 , ,  , all , all 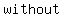 affecting the result affecting the result
the Associative Property-Use the associative property to change the grouping in an algebraic expression to make the work tidier or more convenient.
The commutative property makes working with algebraic expressions easier. The commutative property changes the order of some numbers in an operation to make the work tidier or more convenient all without affecting the result.
Addition: 
Example:  and and  , so , so 
 the numbers the numbers 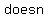 affect the result. affect the result.
Multiplication:
Subtraction:  is not equal to is not equal to  (except in a few special cases) (except in a few special cases)
Example: (5) (+2) = (7) and (+2) (5) = +7, so (5) (+2) is not equal to (+2) (5)
Here, you see how 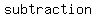 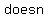 follow the commutative property. follow the commutative property.
Exception: If  and and  are the same number, then the subtraction appears to be commutative because switching the order doesnt change the answer. are the same number, then the subtraction appears to be commutative because switching the order doesnt change the answer.
Example: 2 2 = 0 and 2 + 2 = 0, so 2 2 = 2 + 2
Division:  (except in a few special cases) (except in a few special cases)
Example:  and and  , so , so  is not equal to is not equal to 
Division also 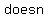 follow the commutative property. follow the commutative property.
Exception: If a and b are opposites, then you get 1 no matter which order you divide them in.
Example: 2 : 2 = 1 and 2:2 = 1, so 2:2 = 2 :2
|
|
|