Question 436796: Please help me find the eXACT solutions of the given equation, in radians, that lie in the interval [0, 2π).
6 cos3(x) + 6 cos(x) = 0
I started it by factoring
6cos(x)*[cos2(x)+cos(x)]=0
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website!  ==> cos3x + cosx = 0 ==> cos3x + cosx = 0
==> cos2x cosx - sin2x sinx + cosx = 0
==> 
==> 
==> 
==> 
==> 
==> cosx = 0 ==> x =  , , 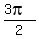 ; ;
==> Also,  , or , or  , , 
==> x =  , , 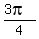 , , 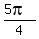 , , 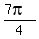 . .
==> Solution set is {  , , 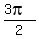 , ,  , , 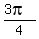 , , 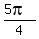 , , 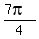 }. }.
|
|
|