Question 436704: A plane flies 1500 miles against the wind in 3 hours and 45 minutes. The return trip with the wind takes 3 hours. Assume that the wind speed stays constant. Find the speed of the wind and the speed of the airplane with no wind.
Found 4 solutions by mananth, ikleyn, josgarithmetic, greenestamps:
Answer by mananth(16949)   (Show Source): (Show Source):
You can put this solution on YOUR website! A plane flies 1500 miles against the wind in 3 hours and 45 minutes. The return trip with the wind takes 3 hours. Assume that the wind speed stays constant. Find the speed of the wind and the speed of the airplane with
no wind.
against wind 3.75 hours
with wind 3.00 hours
Distance = same= 1500
plane speed =x
wind speed =y
t=d/r
1500/(x-y)=3.75
3.75(x-y)=1,500.00
3.75x -3.75y=1500 ....................1
1500/(x +y)=3.00
3.00(x+y)=1500
3.00x+3.00y= 1500 ...............2
Multiply (1) by 9.88
Multiply (2) by 13.00
we get
37.05x-37.05y=14820
39x+39y=19500
76.05x= 34320
/76.05
x=451.28 mph plane speed
plug value of x in (1)
3.75 x-3.75y =1500
1692.31 -3.75y= 1500
-3.75y=1500-1692.31
-3.75y=-192.31
y=51.28 mph wind speed
Answer by ikleyn(53426)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A plane flies 1500 miles against the wind in 3 hours and 45 minutes.
The return trip with the wind takes 3 hours.
Assume that the wind speed stays constant.
Find the speed of the wind and the speed of the airplane with no wind.
~~~~~~~~~~~~~~~~~~~~~~~~~
@mananth solved the problem making tons of unnecessary calculations.
Therefore, his solution can scary a reader and is a bad way to teach.
I will show below a standard solution approach to make minimum calculations.
The flight against the wind took 3 hours and 45 minutes = 3 hours = hours =  hours.
The effective rate was hours.
The effective rate was 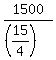 = = 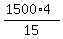 = 100*4 = 400 miles per hour.
It gives you first equation
u - v = 400 mph (1),
since the effective rate against the wind is the difference of the airspeed u and the rate of the wind v.
The flight with the wind took 3 hours.
The effective rate was = 100*4 = 400 miles per hour.
It gives you first equation
u - v = 400 mph (1),
since the effective rate against the wind is the difference of the airspeed u and the rate of the wind v.
The flight with the wind took 3 hours.
The effective rate was 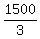 = 500 miles per hour.
It gives you second equation
u + v = 500 mph (2),
since the effective rate with the wind is the sum of the airspeed u and the rate of the wind v.
Now you have a system of two equations for u and v.
To find u, add equations (1) and (2). The terms with 'v' cancel each other, and you will get
2u = 400 + 500 = 900, u = 900/2 = 450.
Now from equation (2) v = 500 - 450 = 50.
Thus the problem is solved, and the ANSWER is
airspeed is 450 mph (the rate in still air, or relative the air), and
the rate of the wind is 50 mph. = 500 miles per hour.
It gives you second equation
u + v = 500 mph (2),
since the effective rate with the wind is the sum of the airspeed u and the rate of the wind v.
Now you have a system of two equations for u and v.
To find u, add equations (1) and (2). The terms with 'v' cancel each other, and you will get
2u = 400 + 500 = 900, u = 900/2 = 450.
Now from equation (2) v = 500 - 450 = 50.
Thus the problem is solved, and the ANSWER is
airspeed is 450 mph (the rate in still air, or relative the air), and
the rate of the wind is 50 mph.
Solved, making the minimum calculations - making only those calculations that are really needed.
-----------------------------
Now, after seeing my solution, it should be clear to you that the answer is the nice round numbers,
while ugly numbers from @mananth are (1) incorrect and (2) are the consequences of his
"approximate" calculations that only harm the solution.
Actually, the input numbers in this problem are "very nice" and lead to the nice
answer, if to treat the problem properly.
The way as I treat the problem in my post is the EXPECTED way on how the problem SHOULD be treated.
Answer by josgarithmetic(39702)   (Show Source): (Show Source):
Answer by greenestamps(13258)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Against the wind, the plane travels the 1500 miles in 3 hours and 45 minutes, or 3 3/4 = 15/4 hours. Its speed is 1500/(15/4) = 400 mph.
With the wind, it travels the 1500 miles in 3 hours; its speed is 1500/3 = 500 mph.
You can of course find the speed of the plane and the speed of the wind using formal algebra. But common sense and simple mental arithmetic lead quickly to the solution.
Adding the speed of the wind to the speed of the plane gives a speed of 500 mph; subtracting the speed of the wind from the speed of the plane gives a speed of 400 mph.
That means the speed of the plane is halfway between those two speeds, which is 450 mph; and that means the speed of the wind is 50 mph.
ANSWERS: plane speed 450 mph, wind speed 50 mph
|
|
|