|
Question 4363: There are three friends named Allan, Bobby and Charlie. The three friends want to know their individual rate in finishing a job. Allan and Bobby can finish the job in 42 days, Bobby and Charlie can finish the job in 31 days, and Allan and Charlie can finish the job in 20 days. Solve the rate of each individual.
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let A = number of days it would take Allan to do the job alone,
Let B = number of days it would take Bobby to do the job alone, and
Let C = number of days it would take Charlie to do the job alone.
 = part of the job that Allan can do in 1 day, = part of the job that Allan can do in 1 day,
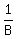 = part of the job that Bobby can do in 1 day, and = part of the job that Bobby can do in 1 day, and
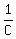 = part of the job that Charlie can do in 1 day. = part of the job that Charlie can do in 1 day.
Also given in the problem,
 = part of the job that Allan and Bobby can do in 1 day, = part of the job that Allan and Bobby can do in 1 day,
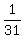 = part of the job that Bobby and Charlie can do in 1 day, and = part of the job that Bobby and Charlie can do in 1 day, and
 = part of the job that Allan and Charlie can do in 1 day. = part of the job that Allan and Charlie can do in 1 day.
There are three unknowns, so there must be three equations to solve:
 = Equation #1 = Equation #1
 = Equation #2 = Equation #2
 = Equation #3 = Equation #3
To eliminate one of these unknowns, Subract Equation #2 - Equation #3, which eliminates the 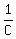

To this equation, now add Equation #1, which eliminates the 



Finding a least common denominator for denominators like 31, 20, and 42 is harder than just using the product of the denominators, which is 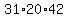 = 26040. The result is as follows: = 26040. The result is as follows:




Divide both sides by 2, giving

To find B, take the reciprocal of both sides:
 , which is approximately 330 days. , which is approximately 330 days.
To find A,




 , which is approximately 48 days. , which is approximately 48 days.
To find C




 , which is approximately 34 days. , which is approximately 34 days.
[NOTE: Where did you get this problem?? If I had known when I started this problem that it would have been this complicated, I would have left it for Kenny!! There is probably an easier way to do this. Ask him!!]
R^2 at SCC
|
|
|
| |