Question 43500: Will you please help me with this word problem. The units digit of a two-digits number is 1 more than 4 times the tens digit. If the digits are reversed, the new number is 5 more than 3 times the original number. Find the original number.
Answer by psbhowmick(878)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the digit in the 10's place be 'x' and that in the unit's place be 'y'.
Then, the number is: 10x + y.
Now, 4 times the digit in 10's = 4x.
According to the problem, digit in unit's place = 4 times digit in ten's place + 1.
So, y = 4x + 1_________(1)
Again, if the digits are reversed then the number becomes: 10y + x.
[As then the digit in 10's place becomes that in unit's place and that in unit's place becomes digit in 10's place]
According to the problem, new number = 3 times original number + 5.
Hence, 10y + x = 3(10x + y) + 5 or 7y - 29x = 5 _________(2)
Substituting the value of 'y' from (1) in (2),
7(4x + 1) - 29x = 5
or 28x + 7 - 29x = 5
or -x = 5 - 7 = -2
or x = 2
Putting x = 2 in (1), we have y = 4(2) + 1 = 9.
Thus, the original number is (10x + y) = 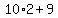 = 29. = 29.
|
|
|