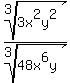 Write as a single cube root:
Write as a single cube root:
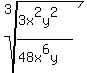 Divide top and bottom by 3, which gives 16 on the bottom
Subtract the exponents of x, getting x4 on the bottom.
Subtract the exponents of y, getting y on the top:
Divide top and bottom by 3, which gives 16 on the bottom
Subtract the exponents of x, getting x4 on the bottom.
Subtract the exponents of y, getting y on the top:
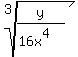 rewrite the 16 as 24
rewrite the 16 as 24
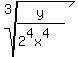 The idea is to get the denominator so that all the exponents will
be divisible by 3, the index of the root
To make 2 have an exponent divisible by 3, we need to multiply it
by 22 so it will have an exponent of 6
To make x have an exponent divisible by 3, we need to multiply it
by x2 so it will have an exponent of 6.
So we multiply under the radical by
The idea is to get the denominator so that all the exponents will
be divisible by 3, the index of the root
To make 2 have an exponent divisible by 3, we need to multiply it
by 22 so it will have an exponent of 6
To make x have an exponent divisible by 3, we need to multiply it
by x2 so it will have an exponent of 6.
So we multiply under the radical by 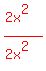
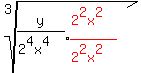 or
or
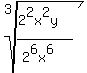 Separate into the quotient of two cube roots again:
Separate into the quotient of two cube roots again:
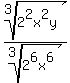 Get rid of the cube root on the bottom by dividing
each exponent by the index 3 of the root:
Get rid of the cube root on the bottom by dividing
each exponent by the index 3 of the root:
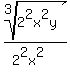 Changing 22's to 4's
Changing 22's to 4's
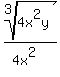 Edwin
Edwin