Question 432597: The length of a rectangle is 4 inches more than the length of the square. The width of the rectangle is 2 inches more than the side of the square. If the sum of the areas of the square and retangle is 64 sq. inches, find the dimensions of the square and the rectangle.
Answer by jorel1380(3719)   (Show Source): (Show Source):
You can put this solution on YOUR website! If the length of a rectangle is 4 in. more than a square,then its' length is x+4. Similarly, its' width is x+2. The sum of the areas, rectangle and square, is 64:
------------
(x+2)(x+4)+x2=64
x2+6x+8+x2=64
2x2+6x-56=0
(2x+14)(x-4)=0
x=-7,4
Throwing out the negative result, our square is 4X4 inches.
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=484 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 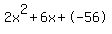 can be factored: can be factored:

Again, the answer is: 4, -7.
Here's your graph:
 |
|
|
|