Question 43248: In triangle ABC, c = 10 and angle A = angle B = 40o. Find the length of the median to line segment AC
Found 2 solutions by psbhowmick, venugopalramana:
Answer by psbhowmick(878)   (Show Source): (Show Source):
You can put this solution on YOUR website! In triangle ABC, BD is the median which bisects the side AC.
Drop a perpendicular from C on AB intersecting AB at E.

In triangle ABC, < CAB = < CBA = 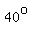 and AB = 10 units. and AB = 10 units.
As triangle ABC is isoscles, so the perpendicular dropped from the vertex on the opposite bisects the opposite side.
Hence, AE = BE = 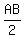 = =  = 5 units. = 5 units.
Now, in triangle AEC, < AEC is right angle.
So, 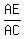 = cos(< CAE) = cos(< CAE)
or 
or 
or 
or 
So, AD =  AC = AC = 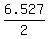 = 3.263 units. = 3.263 units.
Now, consider triangle ADB.
Apply cosine formula
 cos(< BAD) cos(< BAD)
or 
or 
or 
or BD = 7.788 units
Thus, the length of the median to the line segment AC is 7.788 units.
Answer by venugopalramana(3286)   (Show Source): (Show Source):
You can put this solution on YOUR website! In triangle ABC, c = 10 and angle A = angle B = 40o. Find the length of the median to line segment AC
let the median from B to AC be BE=M
AB=10...ANGLE A = ANGLE B =40...HENCE...AC=BC=X SAY...AND ANGLE C=180-40-40=100
10/SIN(100)=X/SIN(40)
X=10*SIN(40)/SIN(100)=6.523=AC=BC
IN TRANGLE BEC
EC=AC/2=3.262
BC=6.523
ANGLE BCE =100
BE^2=BC^2+CE^2-2*BC*CE*COS(BCE)=6.523^2+3.262^2-2*6.523*3.262*COS(100)
BE^2=60.538
BE=7.78
|
|
|