Question 43142: Two planes leave an airport at the same time, one flying due west at 500km/h and the other flying due southeast at 300km/h. What is the distance between the planes two hours later?
Answer by psbhowmick(878)   (Show Source): (Show Source):
You can put this solution on YOUR website! Note: Distance = Speed x Time
In 2 hours, the plane travelling to West travels a distance of 500x2 = 1000 km.
In 2 hours, the plane travelling to South-East travels a distance of 300x2 = 600 km.
If their initial position was the point O then their final positions, after 2 hours, are points A and B respectively.

We need to know the length of AB.
In triangle BCO, as OB is in South-East direction.
So, 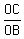 = cos(< BOC) = = cos(< BOC) = 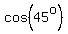
or 
or 
or 
or 
or OC = 424.264 km
Therefore, AC = AO + OC = 1000 + 424.264 = 1424.264 km
As BCO is a right angled isosceles triangle with
Now, in triangle ACB,
Applying Pythagorus theorem,

or 
or 
or 
or AB = 1486.112 km
Hence, the reqd. distance between the two planes after 2 hours is 1486.112 km.
|
|
|