SOLUTION: help me solve using Gauss-Jordan elimination 2xl+4x2-10x3=-2 3xl+9x2-2lx3=0 xl+5x2-12x3=1

2xl+4x2-10x3=-2
3xl+9x2-2lx3=0
1xl+5x2-12x3=1
 

 
The idea is to end up with a matrix that looks like this:
 

 
where there are numbers where the 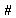's are
 
 
 

Divide row 1 by 2 to get a 1 in the upper left corner
 

 
Get a 0 under it by multiplying row 1 by -3
and adding it to row 2  getting 
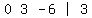Then replace row 2 by that
 

 
Get a 0 in the lower left by multiplying row 1 by -1
and adding it to row 3  getting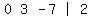 
Then replace row 3 by that

 
Get a 1 where the first 3 on the second row is by
dividing the second row through by 3
 

 
Get a 0 where the 3 is on the bottom row
 by multiplying row 2 by -3
and adding it to row 3  getting 
Then replace row 3 by that

 
Now divide the bottom row through by -1 to
get a 1, and you have the final matrix:
 

 
That means:
 
1x1 + 2x2 - 5x3 = -1
0x1 + 1x2 - 2x3 =  1
0x1 + 0x2 + 1x3 =  1
 
or simplifying,
 
x1 + 2x2 - 5x3 = -1
x2 - 2x3 = 1
x3 = 1
 
Substitute 1 for x3 in the middle equation:
 
 x2 - 2x3 = 1
x2 - 2(1) = 1
   x2 - 2 = 1
       x2 = 3
 
Substitute 1 for x3 and 3 for x1 in the top equation:
 
   x1 + 2x2 - 5x3 = -1
x1 + 2(3) - 5(1) = -1
      x1 + 6 - 5 = -1
          x1 + 1 = -1
              x1 = -2
 
Solution:  (x1,x2,x3) = (-2,3,1)
 
Edwin