SOLUTION: The annual income of residents in a county is $42,000 with a standard deviation of $10,000. Between what two values do 95% of the incomes of county residents lie?

Algebra ->  Probability-and-statistics -> SOLUTION: The annual income of residents in a county is $42,000 with a standard deviation of $10,000. Between what two values do 95% of the incomes of county residents lie?      Log On


   

Question 431234: The annual income of residents in a county is $42,000 with a standard deviation of $10,000. Between what two values do 95% of the incomes of county residents lie?
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
Assuming a normal distribution, then by the empirical rule, 95% of the incomes lie within two standard deviations, or between $22,000 and $62,000.
Assuming non-normality, and using Chebyshev's theorem, then
P%28abs%28X+-+42000%29+%3C=+k%2A10000%29+%3E=+1-1%2Fk%5E2+=+0.95,
==> 1%2Fk%5E2+=+0.05 ==> k+=+2sqrt%285%29
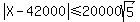
==> abs%28X+-+42000%29+%3C=+20000sqrt%285%29
<==> 42000+-++20000sqrt%285%29%3C=+X+%3C=++42000+%2B+20000sqrt%285%29
Since the left endpoint is negative, the bounds are 0 and 86,721.36.