Question 430947: identify the foci,of the following ellipse. sketch each.
1. (x-1)^2/25 + (y+2)^2/16 = 1
Found 2 solutions by ewatrrr, Gogonati:
Answer by ewatrrr(24785)   (Show Source):
You can put this solution on YOUR website!
Hi
Standard Form of an Equation of an Ellipse is 
where Pt(h,k) is the center and a and b are the respective vertices distances from center.
(x-1)^2/25 + (y+2)^2/16 = 1 | a = 5 and b = 4 C(1,-2)
f = sqrt(25-16) = 3 (foci are located 3 each side of center along major axis)
|foci are (-2,-2) and (4,-2)
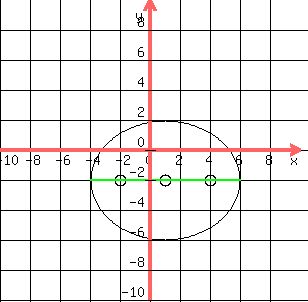
Answer by Gogonati(855)  (Show Source):
You can put this solution on YOUR website! Solution: The center of this ellipse is the point (1, -2), a^2=25 and b^2=16
As we know c^2=a^2-b^2=25-16=9, thus,  , And c=/- sqrt(9)
c=-3 and c=3, hence the coordinates of the foci will be:(-3,0) and (3,0),when the ellipse was centered at (0, 0), Our ellipse was shifted at poit (1, -2), thus the new foci will be:(-3+1, 0-2) and (3+1, 0-2), simplify: (-2, -2) and (4, -2).
Answer: the foci of ellipse are: (-2, -2) and (4, -2)
Done.
|
|
|
