Question 430577: Hello,
I have 4 differnt problems that deal with Substitution Method & Addition Method in which I am hoping you will be able to help me understand how to solve them.
The first one is with Substituion Method   I can't figure out the solution sets.
The second one is with Substituion Method as well  
I cant figure out the solution sets.
The third problem is with Addition Method   i am not sure of the solution sets on this one.
The final problem is with addition method as well   I dont know the solution sets.
If you could please help me with these problems i would REALLYYY appriciate it! I am soooo lost. THANK YOUU!!
Answer by ankor@dixie-net.com(22740)   (Show Source):
You can put this solution on YOUR website! I have 4 different problems that deal with Substitution Method & Addition Method in which I am hoping you will be able to help me understand how to solve them.
The first one is with Substitution Method I can't figure out the solution sets.
Rearrange the 1st equation for substitution
y = (-x+1)
Replace y in the 2nd equation
x^2 + x(-x+1) - (-x+1)^2 = -11
x^2 - x^2 + x - (x^2 - 2x + 1) = -11
Combine like terms
x^2 - x^2 - x^2 + x + 2x - 1 + 11 = 0
-x^2 + 3x + 10 = 0
Change signs, multiply by -1
x^2 - 3x - 10 = 0
Factors to
(x-5)(x+2) = 0
Two solutions, find y for each of them using y = -x+1
x = 5, then y = -5 + 1 = -4
x = -2, then y = -(-2) + 1 = 3
:
:
The second one is with Substitution Method as well
The 2nd equation will be used for substitution
x = (y-6)
Replace x in the 1st equation
(y-6)^2 + y^2 = 180
y^2 - 12y + 36 + y^2 = 180
Combine like terms
y^2 + y^2 - 12y + 36 - 180 = 0
2y^2 - 12y - 144 = 0
Simplify, divide by 2
y^2 - 6y - 72 = 0
Factors to
(y-12)(y+6) = 0
Two solutions
y = 12, then x = 12 - 6 = 6
y = -6, then x = -6 - 6 = -12
;
:
The third problem is with Addition Method
Multiply the 1st equation by 7, multiply the 2nd equation by 3, we have
14x^2 + 21y^2 - 210 = 0
15x^2 - 21y^2 - 51 = 0
----------------------------Addition eliminates y^2, find x
29x^2 - 261 = 0
29x^2 = 261
x^2 =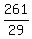 
x^2 = 9
x = 3
Find y using the original 1st equation
2(3^2) + 3y^2 - 30 = 0
18 + 3y^2 - 30 = 0
3y^2 - 12 = 0
3y^2 = 12
y^2 = 
y^2 = 4
y = 2
:
:
The final problem is with addition method as well
Multiply the 2nd equation by -1, arrange as follows
x^2 + y^2 = 16
0x^2 -y^2 + 3x = -16
-----------------------adding eliminates y^2 find x
x^2 + 3x = 0
Factor out x
x(x+3) = 0
Two solutions
x = 0
x = -3
Find y using the 1st equation
When x=0
0 + y^2 = 16
y = 4
When x=-3
-3^2 + y^2 = 16
y^2 = 16 - 9
y^2 = 7
y = 
:
You should check these solutions in the original equations, a lot of math here
mistakes are made, so check my work.
|
|
|
