|
Question 4303: name the quadrant in which the point (4, -70) lies
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! As illustrated by Earlsdon, the problem is a difference of squares:
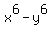
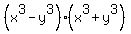
I thought it was strange that Earlsdon did not finish the problem by factoring the difference and sum of cubes that results from this. Then I looked again and I noticed that your question was NOT to actually factor the problem completely. Instead, you asked the question, "How would I start?" That is exactly what he did--he got you started!! I'm sure if he were tuned in right now, he'd be glad to finish it for you.
First, throughout my career, I have often thought about a tradition of math related to the factoring of the difference of squares. Of course it goes like this:

Or should it be written like this:
 with the with the 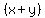 factor written first? factor written first?
Of course both ways are completely acceptable by the commutative property, but I always tried to write it the same for my own consistency in teaching. Moreover, I always preferred to write the (x-y) first, but I never knew why! Finally I noticed that if you write the difference of squares formula with the (x-y) first, it makes it easier to remember the difference and sum of cubes formulas when you get to those.
Here are the three (or four) formulas:
Difference of squares:

 (It can be factored, but not in this level of math!) (It can be factored, but not in this level of math!)


To help remember these formulas, remember that with the
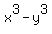 formula, you always start off with the formula, you always start off with the 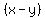 factor, just like I prefer to do in writing the difference of squares formula. factor, just like I prefer to do in writing the difference of squares formula.
With the  , you always start off with the , you always start off with the 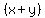 factor. factor.
Next notice that in BOTH formulas it is a binomial multiplied by a trinomial. The trinomial that follows in BOTH formulas is nearly the same having a factor with 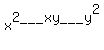 . The only differences in the two formulas are two signs. The first sign in the trinomial is always the opposite of the sign in the binomial, and the second sign in the trinomial is always positive. Makes it easy to remember, and when you start getting older, that is really important, right? . The only differences in the two formulas are two signs. The first sign in the trinomial is always the opposite of the sign in the binomial, and the second sign in the trinomial is always positive. Makes it easy to remember, and when you start getting older, that is really important, right?
So there you have it:
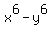 which is a difference of two squares. which is a difference of two squares.
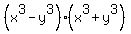 , which is itself a difference and a sum of cubes. , which is itself a difference and a sum of cubes.
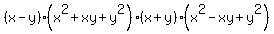
R^2 from SCC
|
|
|
| |