|
Question 428893: find the vertices,foci and equation of asymptotes of x^2-2y^2=2 for the hyperbola
Answer by lwsshak3(11628)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the vertices,foci and equation of asymptotes of x^2-2y^2=2 for the hyperbola
..
Standard form of hyperbola with horizontal transverse axis(opens sideways):
(x-h)^2a^2-(y-k)^2/b^2=1
Standard form of hyperbola with Vertical transverse axis(opens up and down):
(y-k)^2a^2-(x-h)^2/b^2=1
(h,k)=(xy) coordinates of the center for both forms
..
Given:
x^2-2y^2=2
=x^2/2-y^2/1=1
This is a hyperbola with a horizontal transverse axis and center at (0.0)
a^2=2
a=sqrt(2)
b^2=1
b=1
c^2=a^2+b^2=2+1=3
c=sqrt(3)
..
The vertices are on the transverse axis located +- a from the center or (0,sqrt(2)) & (0,-sqrt(2))
Foci are also on the transverse axis just inside the vertices locate =-c from the center or (0,sqrt(3)) & (0,-sqrt(3))
..
When figuring the asymptotes you can think of straight lines with slope+- b/a for hyperbolas with horizontal transverse axis and slope +-b/a for hyperbolas with vertical transverse axis. And they all go thru the center of the hyperbola. For this reason, you can use the standard form of a straight line, y=mx+b, to get the equations of the hyperbolas. knowing the slope and and a point, the center, on the line. In the given case, equations of the asymptotes are: y=sqrt(2)/2x and y=-sqrt(2)/2x (note that in this case the y-intercept, b=0)
..
ans:
vertices:(0,sqrt(2)) & (0,-sqrt(2))
Foci: (0,sqrt(3)) & (0,-sqrt(3))
equation of asymptotes: y=.707x and y=-.707x
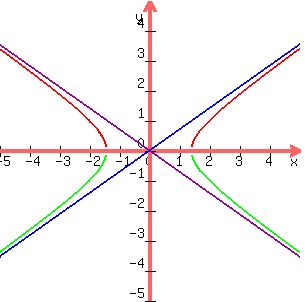
The graph below can serve as a check on these answers:
..
y=+-((x^2-2)/2)^.5
|
|
|
| |